
在“着色”章节,我们看到了一个物体的表面法向量如何对它的外观效果产生巨大的影响,例如,正确选择法线可以使多面体看起来平滑弯曲,这是因为正确选择法线会改变光与表面相互作用的方式,从而改变我们的大脑对物体形状的猜测方式。不幸的是,通过插值法线,除了使曲面看起来平滑弯曲外,我们还能做的并不多。
在“纹理”章节,我们看到了如何通过在表面上“绘画”来添加虚假的细节。这种技术称为纹理映射(texture mapping),它为我们提供了对表面更细粒度的控制。然而,纹理映射不会改变三角形的形状——它们仍然是平的。
法线映射(normal mapping)
结合了这两种思想。我们可以使用法线来改变光与表面相互作用的方式,从而改变表面的形状,我们可以使用属性映射将属性的不同值分配给三角形的不同部分。通过结合这两种想法,法线映射可以让我们在像素级别定义表面法线。
法线贴图(normal map)与每个三角形相关联,法线贴图类似纹理贴图,但其元素是法线向量而不是颜色,在渲染时,我们不是像冯氏着色那样计算内插法线,而是使用法线贴图为我们正在渲染的某个像素获取法线向量,就像纹理映射为该特定像素获取颜色一样。然后我们使用这个向量来计算像素的光照。



上面这3幅图都是使用带有纹理的平面正方形(两个三角形)的渲染效果。
当我们添加法线贴图和进行适当的逐像素着色时,我们会产生额外的几何细节的错觉,菱形的着色取决于入射光的方向,我们的大脑将其解释为菱形是有体积的。
有几个实际注意事项需要牢记。首先,法线贴图中向量的方位是相对于它们所应用的三角形表面的。用于此的坐标系称为切空间(tangent space),其中两个轴(通常是和)与表面相切(嵌入),剩下的向量垂直于表面。在渲染时,将相机空间中表示的三角形的法向量根据法线贴图中的向量进行修改,得到一个最终用于光照方程的法向量。这使得法线贴图独立于场景中物体的位置和方位。

其次,一种非常流行的编码法线贴图的方法是将法线作为纹理,将、和的值映射到、和值。这使法线贴图具有非常典型的紫色外观,因为紫色是红色和蓝色(没有绿色)的组合,它用于对表面的平坦区域进行编码。
虽然这种技术可以极大地提高场景中表面的感知复杂性,但它也不是没有限制的。例如,由于使用法线映射的平面依然保持着平面的特征,它不能改变物体的轮廓。出于同样的原因,当从一个极端的角度或近距离观察法线映射的表面时,或者法线贴图所表现的特征所占用的尺寸大小,明显与物体表面的尺寸大小不一致时,这种法线贴图所营造出的视觉错觉就会消失。这种技术更适合细微的细节,比如皮肤上的毛孔、粉刷墙壁上的图案,或者橘子皮不规则的外观。因此,这种技术也被称为
凹凸映射(bump mapping)。
我们开发的光线追踪渲染器最显著的特点之一是能够显示物体之间的反射。我们也可以在光栅化渲染器中创建一个相对令人信服但有点儿虚假的反射实现。
想象一下,我们有一个代表房子中房间的场景,我们想要渲染放置在房间中间的反射物体。对于表示该物体表面的每个像素,我们知道它所表示的点的3D坐标、表面法线,并且由于我们知道相机的位置,我们还可以计算到该点的视线向量。我们可以根据表面法线反射视线向量来获得反射向量,就像我们在第4章“阴影和反射”中做的那样。
此时,我们想知道来自反射向量方向的光的颜色。如果这是一个光线追踪渲染器,我们只需沿着那个方向追踪射线并找出答案。但是,这不是光线追踪渲染器。我们该怎么办?
环境映射(environment mapping)
为这个问题提供了一个可能的答案。假设在渲染房间内的物体之前,我们将一个相机放在它的中间并渲染场景6次——每个垂直方向(上、下、左、右、前、后)一次。你可以想象相机在一个假想的立方体中,立方体的每一面都是其中一个渲染的视口。我们将这6个渲染结果保存为纹理。我们称这6个纹理的集合为
立方体贴图(cube map),这就是为什么这种技术也被称为
立方体映射(cube mapping)。
立方体贴图是
环境贴图的一种常见形式,还有一种常见形式是
球面贴图(sphere map),其对应的映射被称为
球面映射(sphere mapping)。
然后我们渲染反射物体。当我们需要反射颜色时,我们可以使用反射向量的方向来选择立方体贴图的其中一个纹理,然后使用该纹理的纹素来获得在该方向上看到的颜色的近似值——无须追踪任何射线!
这种技术有一些缺点,如 立方体贴图从单个点捕捉场景的外观 。如果我们渲染的反射物体不在那个点,反射物体的位置就不会完全符合我们的预期,所以很明显这只是一个近似值。如果反射物体在房间内移动,这一缺点会特别明显,因为反射场景不会随着物体移动而改变。
如果“房间”足够大并且离物体足够远(如果物体的运动相对于房间的大小来说可忽略),那么真正的反射和预渲染的环境贴图之间的差异可能会被忽视。但这种技术对于表示深空中具有反射性的宇宙飞船的场景非常有效,因为“房间”(遥远的恒星和星系)对于所有实际目标渲染物体来说都是无限远的。
还有一个缺点是,我们不得不将场景中的物体分成两类:属于“房间”一部分的静态物体(可以在反射渲染效果中看到),以及具有反射性的动态物体。在某些情况下,这种分类可能很清楚(墙壁和家具是房间的一部分,而人不是),即便如此,动态物体也不会表现在其他动态物体的反射效果中。
值得一提的最后一个缺点与立方体贴图的分辨率有关。虽然在光线追踪渲染器中,我们可以追踪非常精确的反射,但是在立方体映射的情况下,我们需要在精度(高分辨率的立方体贴图纹理产生更清晰的反射)和内存消耗(高分辨率的立方体贴图纹理需要更多的内存)之间做出权衡。在实践中,这意味着环境贴图不会产生与真实光线追踪反射一样清晰的反射,尤其是在近距离观察反射物体时。
我们开发的光线追踪渲染器具有几何上正确、定义非常明确的阴影。这些是对核心算法的非常自然的扩展。光栅化渲染器的架构使得实现阴影稍微复杂一些,但并非不可能。
我们先把要解决的问题形式化。为了正确地渲染阴影,每次我们为像素和光源计算光照方程时,我们都需要知道像素是否真的被光源照亮,或者它是否处于物体相对于该光源的阴影中。
使用光线追踪渲染器,我们可以通过追踪从物体表面到光源的射线来回答这个问题。在光栅化渲染器中,我们没有这样的工具,所以我们必须采取不同的方法。下面我们来探索两种不同的实现方法。
模板阴影(stencil shadow)是一种用非常清晰的边缘来渲染阴影的技术(想象一下在阳光明媚的日子里物体投射的阴影)。这些通常被称为硬阴影(hard shadow)。
我们的光栅化渲染器在唯一一个渲染通道(pass)中渲染场景,它遍历场景中的每个三角形并将其渲染在画布上,每次计算完整的光照方程(基于每个三角形、每个顶点或每个像素,取决于着色算法)。在此过程结束时,画布就有了场景的最终渲染效果。
我们将首先修改光栅化渲染器,从而可以在多个渲染通道中渲染场景,场景中的每个光源(包括环境光)各使用一个渲染通道。和以前一样,每个渲染通道都会遍历每个三角形,但它在计算光照方程时只考虑与此通道相关的光源。
这为我们提供了一组分别由每个光源照亮的场景的图像。我们可以将它们组合在一起,也就是说,逐个像素地对它们求和,为我们提供场景的最终渲染。这个最终图像与单通道版本产生的图像完全相同。下图显示了我们参考场景的3个光源渲染通道的结果和最终的合成结果。



这样我们就可以将“渲染具有多个光源阴影的场景”的目标简化为“多次渲染具有单个光源阴影的场景”。现在我们需要找到一种方法来渲染由单个光源照亮的场景,同时让该光源阴影中的像素完全为黑色。
为此,我们引入了
模板缓冲(stencil buffer)。与深度缓冲一样,它与画布具有相同的尺寸,但其元素是整数。我们可以将其用作渲染运算的模板,例如,仅当模板缓冲区中所保存的相应的值为0时,才修改我们的渲染代码从而在画布上绘制像素。
如果我们可以设置模板缓冲,使被照亮的像素所对应的模板缓冲区的值为0,而阴影中的像素所对应的模板缓冲区的值为非零值,我们就可以使用它来仅绘制被照亮的像素。
要设置模板缓冲区,我们使用一种称为
阴影体(shadow volume)
的东西。阴影体是一个3D多边形,它把处于光源阴影的这部分场景空间包围起来。
我们为每个可能在场景中投射阴影的物体构建一个阴影体。首先,我们确定哪些边缘是物体轮廓的一部分,这些边缘指的是正面三角形和背面三角形之间的边。我们可以使用点积对三角形进行分类,就像我们在“对背面剔除技术”所做的那样。然后,对于每一条边,我们将它们沿着光的方向“挤出”,一直延伸到无穷远。或者,实际上,延伸到场景之外的一个非常远的距离。
这给了我们阴影体的“侧面”。阴影体的“正面”是由物体自身的正面三角形构成的,而阴影体的“背面”可以通过创建一个多边形来计算,该多边形的边是被挤压边的“远”边。
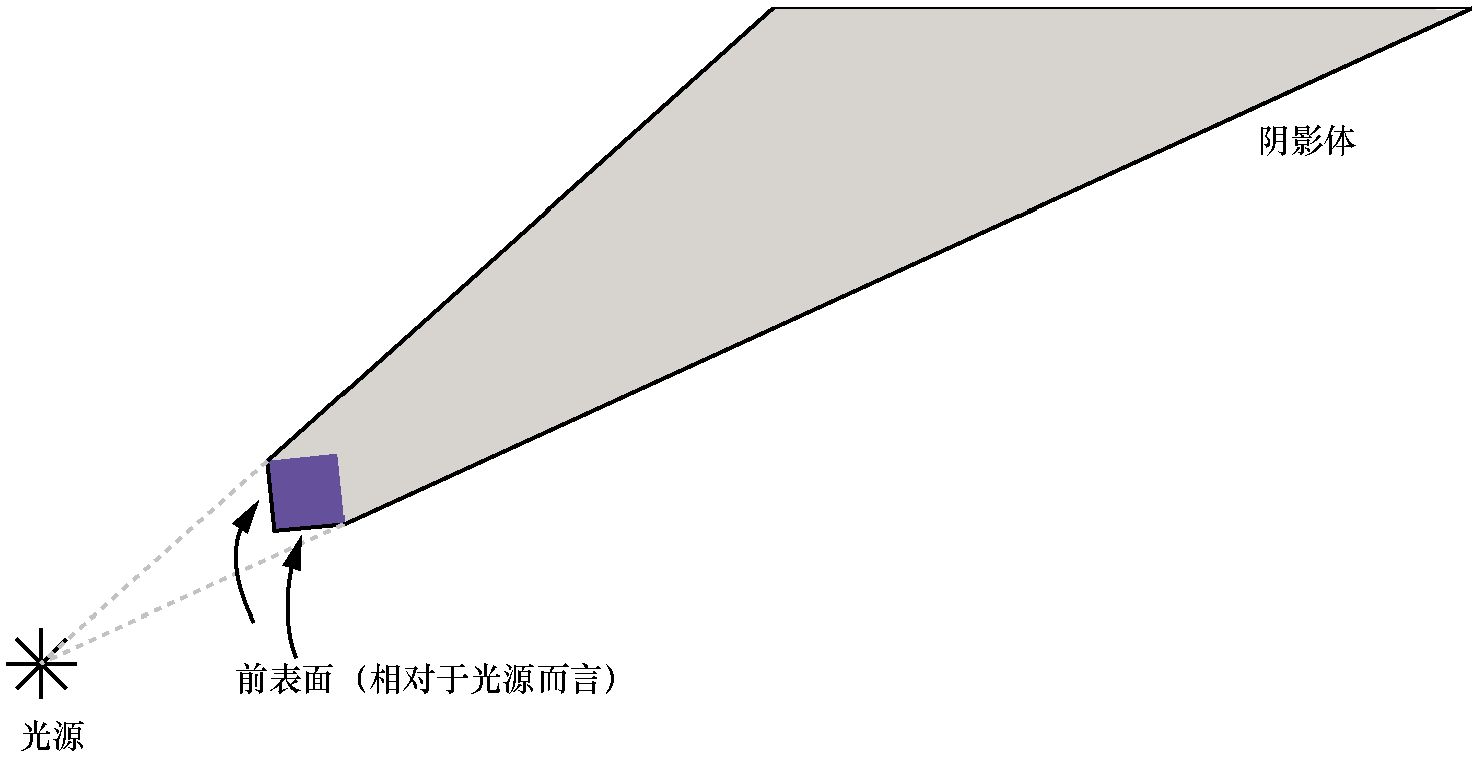
接下来,我们将看到如何使用阴影体来确定画布中的哪些像素相对于光源而言处于阴影中。
想象一条射线从相机处出发进入场景,直到它碰到一个物体表面。在这个过程中,它可能会多次进入并离开阴影体。
我们可以用一个从0开始计数的计数器来跟踪射线进出的次数。射线进入阴影体时,我们就增加计数器的值。射线离开阴影体,我们就减少计数器的值。当射线碰到一个表面时,我们就停下来看一下计数器的值。如果计数值是0,意味着射线进入阴影体和离开阴影体的次数一样多,所以这个点必须被光源照亮;如果它不为0,就意味着射线至少在一个阴影体中,所以这个点一定在阴影中。
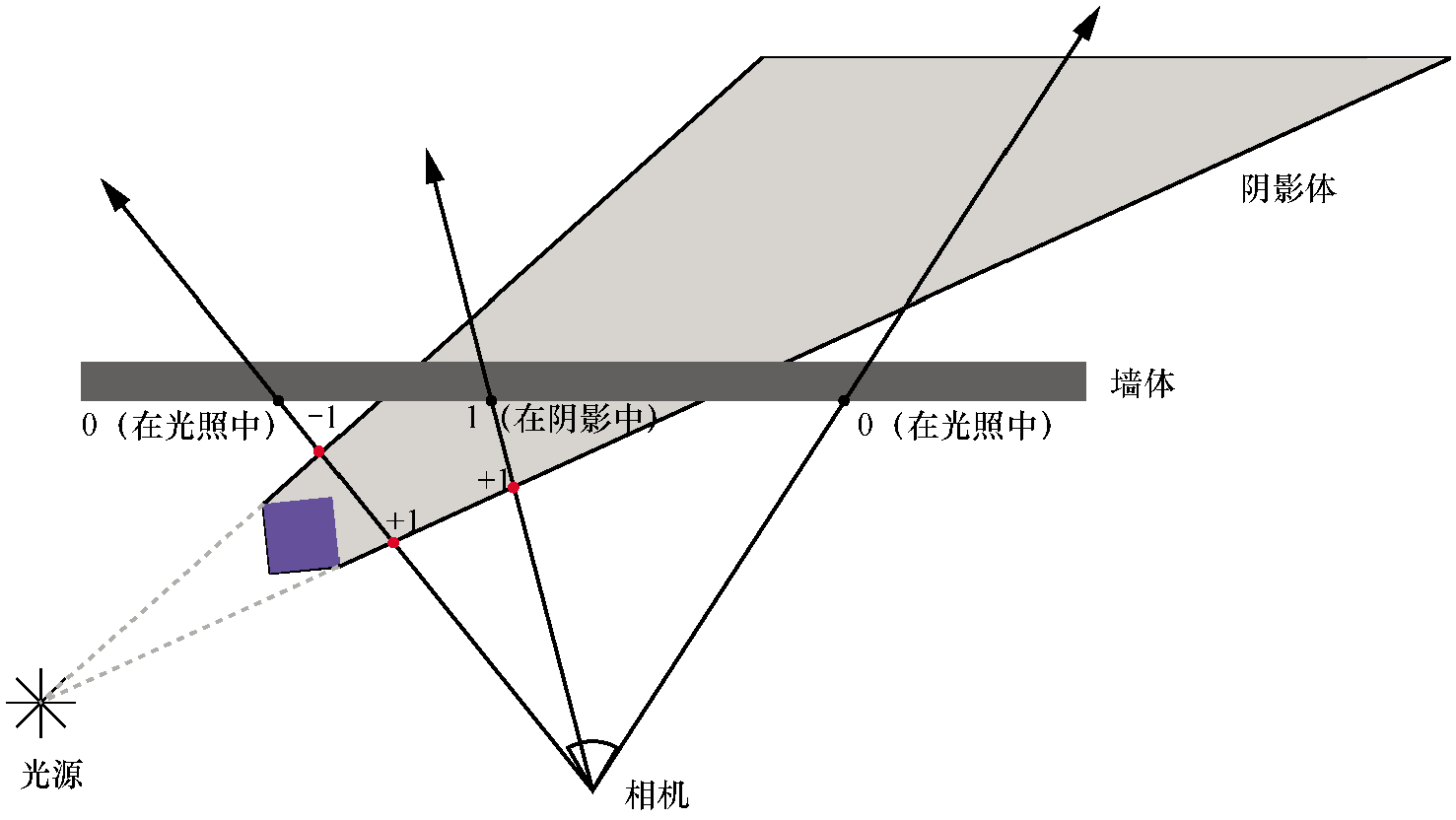
然而,上述讨论只在相机本身不在阴影体内部的情况下才有效!如果射线从阴影体内部开始,并且在到达其表面之前没有离开,我们的算法就会错误地得出物体表面上该点被照亮的结论。
我们可以检查这种情况并相应地调整计数器,但计算一个点处于多少个阴影体内部是一项耗时的操作。幸运的是,有一种更简单、成本更低的方法可以打破这种限制,尽管这种方法有些违背直觉。
射线是无限的,但阴影体不是。这意味着射线从阴影体之外开始则在阴影体外结束。这还意味着射线进入阴影体的次数总是与离开它的次数一样多,跟踪射线的计数器的值必须始终为0。
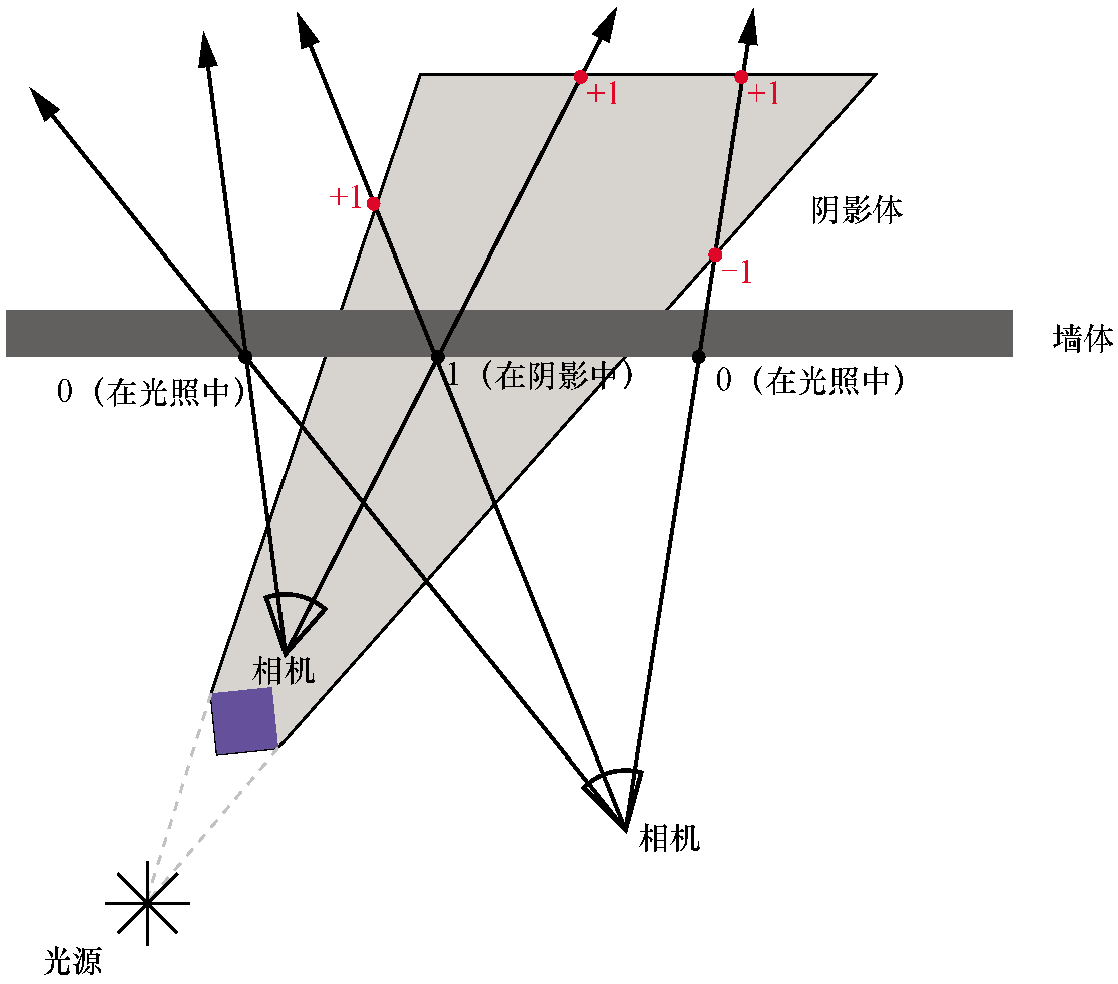
可以看见,与阴影体有奇数个交点的说就是相机在阴影体内,偶数个交点则相机在阴影体外。
我们使用的是光栅化渲染器,而不是光线追踪渲染器,所以我们需要找到一种方法来记录这些计数器,而不需要实际计算射线和阴影体之间的任何交点。我们可以通过模板缓冲区来实现这一点。
首先,我们将场景渲染为仅由环境光照亮。环境光不会投射阴影,因此我们可以在不更改光栅化渲染器的情况下执行此操作。这为我们提供了最终渲染所需的图像,但它也为我们提供了从相机看到的场景的深度信息(包含在深度缓冲区中)。我们需要为后续步骤保留这个深度缓冲区。
接下来,对于每个光源,我们遵循以下步骤。
请注意,在“渲染”步骤中,我们只对修改模板缓冲区感兴趣,无须将像素写入画布,因此也无须计算光照或纹理。我们也不将像素写入深度缓冲区,因为阴影体的侧面实际上并不是场景中的物理物体。相反,我们使用在环境光光照通道内计算的深度缓冲区。
执行此操作后,对于被照亮的像素,模板缓冲区具有零值,对于处于阴影中的像素,则模板缓冲区具有非零值。因此,我们正常渲染场景,由与此通道对应的单个光源照亮,仅在模板缓冲区值为0的像素上调用PutPixel。
对每个光源重复这个过程,我们最终会得到一组图像,它们对应于每个光源照亮的场景,并会正确地考虑阴影。最后一步是将所有图像逐个像素地合成为最终渲染的场景。
使用模板缓冲区来渲染阴影的想法可以追溯到20世纪90年代初期,但最初的实现有几个缺点。基于深度检测的算法变体在1999年~2000年多次被独立发现,其中最著名的是约翰·卡马克在开发《毁灭战士3》时发现的,这就是该变体也被称为卡马克反转(Carmack’s reverse)的原因。
在光栅化渲染器中渲染阴影的另一种众所周知的技术称为阴影映射(shadow mapping)。这使得阴影的边缘不那么清晰(想象物体在阴天投射的阴影)。这些通常被称为软阴影(soft shadow)。
重申一下,我们要回答的问题是,给定表面上的一个点和一个光源,该点是否会受到该光源的光照?这相当于判断光源和点之间是否有物体。
使用光线追踪渲染器,我们追踪了从点到光源的射线。从某种意义上说,我们是在问这个点是否可以“看到”光源,或者等价地,光源是否可以“看到”这个点。
这就引出了阴影映射的核心思想。我们从光源的角度渲染场景,保留深度缓冲区。与我们前文描述的创建环境贴图的方式类似,我们将场景渲染6次,最终得到6个深度缓冲区。这些深度缓冲区,我们称之为阴影贴图(shadow map),让我们可以确定光源在任何给定方向上可以“看到”的最近表面的距离。
对于方向光来说,情况稍微复杂一些,因为它们没有可渲染的位置。相反,我们需要从一个方向渲染场景。这需要使用正交投影(orthographic projection)而不是我们通常的透视投影(perspective projection)。使用透视投影和点光源,每条射线都从一个点开始;使用正交投影和方向光,每条射线彼此平行,共享相同的方向。
当我们想确定一个点是否在阴影中时,我们可以计算从光源到该点的距离和方向。我们使用该方向在阴影贴图中查找相应项。如果从阴影贴图中得到的深度值小于该点到光源的距离,则表示有一个表面比我们照亮的点更靠近光源,因此该点在该表面的阴影中。否则,光源可以“看到”不受阻碍的点,因此该点被光源照亮。
请注意,阴影贴图的分辨率有限,通常低于画布的。根据点和光源的距离和相对方向,阴影贴图分辨率低的问题可能会导致阴影看起来像块状。为了避免这种情况出现,我们也可以对当前采样点周围的深度进行采样,并确定该点是否位于阴影的边缘(可以通过周围的深度不连续性证明)。如果是这种情况,我们可以使用一种类似于双线性滤波的技术,就像我们在“纹理”章节中做的那样,得到一个介于0.0和1.0之间的值,表示这个点在光源下的可见程度,然后将其乘光源的光照度,这使得阴影映射所创建的阴影具有其特有的模糊外观。其他避免块状外观的方法包括用不同的方法对阴影贴图进行采样,例如,可以查看百分比渐进过滤(percentage closer filtering)的相关内容。
<!--
!!html_title Rasterized spheres demo - Computer Graphics from scratch
-->
# Rasterized spheres demo
This demo uses the rasterizer to render the scene used to test the raytracer.
<div class="centered">
<canvas id="canvas" width=600 height=600 style="border: 1px grey solid"></canvas>
</div>
<script>
"use strict";
// ======================================================================
// Low-level canvas access.
// ======================================================================
let canvas = document.getElementById("canvas");
let canvas_context = canvas.getContext("2d");
let canvas_buffer = canvas_context.getImageData(0, 0, canvas.width, canvas.height);
// A color.
function Color(r, g, b) {
return {
r, g, b,
mul: function(n) { return new Color(this.r*n, this.g*n, this.b*n); },
};
}
// The PutPixel() function.
function PutPixel(x, y, color) {
x = canvas.width/2 + (x | 0);
y = canvas.height/2 - (y | 0) - 1;
if (x < 0 || x >= canvas.width || y < 0 || y >= canvas.height) {
return;
}
let offset = 4*(x + canvas_buffer.width*y);
canvas_buffer.data[offset++] = color.r;
canvas_buffer.data[offset++] = color.g;
canvas_buffer.data[offset++] = color.b;
canvas_buffer.data[offset++] = 255; // Alpha = 255 (full opacity)
}
// Displays the contents of the offscreen buffer into the canvas.
function UpdateCanvas() {
canvas_context.putImageData(canvas_buffer, 0, 0);
}
// ======================================================================
// Depth buffer.
// ======================================================================
let depth_buffer = Array();
depth_buffer.length = canvas.width * canvas.height;
function UpdateDepthBufferIfCloser(x, y, inv_z) {
x = canvas.width/2 + (x | 0);
y = canvas.height/2 - (y | 0) - 1;
if (x < 0 || x >= canvas.width || y < 0 || y >= canvas.height) {
return false;
}
let offset = x + canvas.width*y;
if (depth_buffer[offset] == undefined || depth_buffer[offset] < inv_z) {
depth_buffer[offset] = inv_z;
return true;
}
return false;
}
// ======================================================================
// Data model.
// ======================================================================
// A Point.
function Pt(x, y, h) {
return {x, y, h};
}
// A 3D vertex.
function Vertex(x, y, z) {
return {
x, y, z,
add: function(v) { return new Vertex(this.x + v.x, this.y + v.y, this.z + v.z); },
sub: function(v) { return new Vertex(this.x - v.x, this.y - v.y, this.z - v.z); },
mul: function(n) { return new Vertex(this.x*n, this.y*n, this.z*n); },
dot: function(vec) { return this.x*vec.x + this.y*vec.y + this.z*vec.z; },
length: function() { return Math.sqrt(this.dot(this)); },
}
}
// A 4D vertex (a 3D vertex in homogeneous coordinates).
function Vertex4(arg1, y, z, w) {
if (y == undefined) {
this.x = arg1.x;
this.y = arg1.y;
this.z = arg1.z;
this.w = arg1.w | 1;
} else {
this.x = arg1;
this.y = y;
this.z = z;
this.w = w;
}
this.add = function(v) { return new Vertex4(this.x + v.x, this.y + v.y, this.z + v.z); };
this.sub = function(v) { return new Vertex4(this.x - v.x, this.y - v.y, this.z - v.z, this.w - v.w); };
this.mul = function(n) { return new Vertex4(this.x*n, this.y*n, this.z*n, this.w); };
this.dot = function(vec) { return this.x*vec.x + this.y*vec.y + this.z*vec.z; };
this.cross = function(v2) { return new Vertex4(this.y*v2.z - this.z*v2.y, this.z*v2.x - this.x*v2.z, this.x*v2.y - this.y*v2.x); };
this.length = function() { return Math.sqrt(this.dot(this)); };
}
// A 4x4 matrix.
function Mat4x4(data) {
return {data};
}
const Identity4x4 = new Mat4x4([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]]);
// A Triangle.
function Triangle(indexes, color, normals) {
return {indexes, color, normals}
}
// A Model.
function Model(vertices, triangles, bounds_center, bounds_radius) {
return {vertices, triangles, bounds_center, bounds_radius};
}
// An Instance.
function Instance(model, position, orientation, scale, specular) {
this.model = model;
this.position = position;
this.orientation = orientation || Identity4x4;
this.scale = scale || 1.0;
this.specular = specular || 50;
this.transform = MultiplyMM4(MakeTranslationMatrix(this.position), MultiplyMM4(this.orientation, MakeScalingMatrix(this.scale)));
}
// The Camera.
function Camera(position, orientation) {
this.position = position;
this.orientation = orientation;
this.clipping_planes = [];
}
// A Clipping Plane.
function Plane(normal, distance) {
return {normal, distance};
}
// A Light.
const LT_AMBIENT = 0;
const LT_POINT = 1;
const LT_DIRECTIONAL = 2;
function Light(type, intensity, vector) {
return {type, intensity, vector};
}
// ======================================================================
// Linear algebra and helpers.
// ======================================================================
// Makes a transform matrix for a rotation around the OY axis.
function MakeOYRotationMatrix(degrees) {
let cos = Math.cos(degrees*Math.PI/180.0);
let sin = Math.sin(degrees*Math.PI/180.0);
return new Mat4x4([[cos, 0, -sin, 0],
[ 0, 1, 0, 0],
[sin, 0, cos, 0],
[ 0, 0, 0, 1]])
}
// Makes a transform matrix for a translation.
function MakeTranslationMatrix(translation) {
return new Mat4x4([[1, 0, 0, translation.x],
[0, 1, 0, translation.y],
[0, 0, 1, translation.z],
[0, 0, 0, 1]]);
}
// Makes a transform matrix for a scaling.
function MakeScalingMatrix(scale) {
return new Mat4x4([[scale, 0, 0, 0],
[ 0, scale, 0, 0],
[ 0, 0, scale, 0],
[ 0, 0, 0, 1]]);
}
// Multiplies a 4x4 matrix and a 4D vector.
function MultiplyMV(mat4x4, vec4) {
let result = [0, 0, 0, 0];
let vec = [vec4.x, vec4.y, vec4.z, vec4.w];
for (let i = 0; i < 4; i++) {
for (let j = 0; j < 4; j++) {
result[i] += mat4x4.data[i][j]*vec[j];
}
}
return new Vertex4(result[0], result[1], result[2], result[3]);
}
// Multiplies two 4x4 matrices.
function MultiplyMM4(matA, matB) {
let result = new Mat4x4([[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]);
for (let i = 0; i < 4; i++) {
for (let j = 0; j < 4; j++) {
for (let k = 0; k < 4; k++) {
result.data[i][j] += matA.data[i][k]*matB.data[k][j];
}
}
}
return result;
}
// Transposes a 4x4 matrix.
function Transposed(mat) {
let result = new Mat4x4([[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]);
for (let i = 0; i < 4; i++) {
for (let j = 0; j < 4; j++) {
result.data[i][j] = mat.data[j][i];
}
}
return result;
}
// ======================================================================
// Rasterization code.
// ======================================================================
// Scene setup.
let viewport_size = 1;
let projection_plane_z = 1;
function Interpolate(i0, d0, i1, d1) {
if (i0 == i1) {
return [d0];
}
let values = [];
let a = (d1 - d0) / (i1 - i0);
let d = d0;
for (let i = i0; i <= i1; i++) {
values.push(d);
d += a;
}
return values;
}
function DrawLine(p0, p1, color) {
let dx = p1.x - p0.x, dy = p1.y - p0.y;
if (Math.abs(dx) > Math.abs(dy)) {
// The line is horizontal-ish. Make sure it's left to right.
if (dx < 0) { let swap = p0; p0 = p1; p1 = swap; }
// Compute the Y values and draw.
let ys = Interpolate(p0.x, p0.y, p1.x, p1.y);
for (let x = p0.x; x <= p1.x; x++) {
PutPixel(x, ys[(x - p0.x) | 0], color);
}
} else {
// The line is verical-ish. Make sure it's bottom to top.
if (dy < 0) { let swap = p0; p0 = p1; p1 = swap; }
// Compute the X values and draw.
let xs = Interpolate(p0.y, p0.x, p1.y, p1.x);
for (let y = p0.y; y <= p1.y; y++) {
PutPixel(xs[(y - p0.y) | 0], y, color);
}
}
}
function DrawWireframeTriangle(p0, p1, p2, color) {
DrawLine(p0, p1, color);
DrawLine(p1, p2, color);
DrawLine(p0, p2, color);
}
// Converts 2D viewport coordinates to 2D canvas coordinates.
function ViewportToCanvas(p2d) {
return new Pt(
p2d.x * canvas.width / viewport_size | 0,
p2d.y * canvas.height / viewport_size | 0);
}
// Converts 2D canvas coordinates to 2D viewport coordinates.
function CanvasToViewport(p2d) {
return new Pt(
p2d.x * viewport_size / canvas.width,
p2d.y * viewport_size / canvas.height);
}
function ProjectVertex(v) {
return ViewportToCanvas(new Pt(
v.x * projection_plane_z / v.z,
v.y * projection_plane_z / v.z));
}
function UnProjectVertex(x, y, inv_z) {
let oz = 1.0 / inv_z;
let ux = x*oz / projection_plane_z;
let uy = y*oz / projection_plane_z;
let p2d = CanvasToViewport(Pt(ux, uy));
return new Vertex(p2d.x, p2d.y, oz);
}
// Sort the points from bottom to top.
// Technically, sort the indexes to the vertex indexes in the triangle from bottom to top.
function SortedVertexIndexes(vertex_indexes, projected) {
let indexes = [0, 1, 2];
if (projected[vertex_indexes[indexes[1]]].y < projected[vertex_indexes[indexes[0]]].y) { let swap = indexes[0]; indexes[0] = indexes[1]; indexes[1] = swap; }
if (projected[vertex_indexes[indexes[2]]].y < projected[vertex_indexes[indexes[0]]].y) { let swap = indexes[0]; indexes[0] = indexes[2]; indexes[2] = swap; }
if (projected[vertex_indexes[indexes[2]]].y < projected[vertex_indexes[indexes[1]]].y) { let swap = indexes[1]; indexes[1] = indexes[2]; indexes[2] = swap; }
return indexes;
}
function ComputeTriangleNormal(v0, v1, v2) {
let v0v1 = v1.sub(v0);
let v0v2 = v2.sub(v0);
return v0v1.cross(v0v2);
}
function ComputeIllumination(vertex, normal, camera, lights, specular) {
let illumination = 0;
for (let l = 0; l < lights.length; l++) {
let light = lights[l];
if (light.type == LT_AMBIENT) {
illumination += light.intensity;
continue;
}
let vl;
if (light.type == LT_DIRECTIONAL) {
let cameraMatrix = Transposed(camera.orientation);
let rotated_light = MultiplyMV(cameraMatrix, new Vertex4(light.vector));
vl = rotated_light;
} else if (light.type == LT_POINT) {
let cameraMatrix = MultiplyMM4(Transposed(camera.orientation), MakeTranslationMatrix(camera.position.mul(-1)));
let transformed_light = MultiplyMV(cameraMatrix, new Vertex4(light.vector));
vl = vertex.mul(-1).add(transformed_light);
}
// Diffuse component.
let cos_alpha = vl.dot(normal) / (vl.length() * normal.length());
if (cos_alpha > 0) {
illumination += cos_alpha * light.intensity;
}
// Specular component.
let reflected = normal.mul(2*normal.dot(vl)).sub(vl);
let view = camera.position.sub(vertex);
let cos_beta = reflected.dot(view) / (reflected.length() * view.length());
if (cos_beta > 0) {
illumination += Math.pow(cos_beta, specular) * light.intensity;
}
}
return illumination;
}
const SM_FLAT = 0;
const SM_GOURAUD = 1;
const SM_PHONG = 2;
const ShadingModel = SM_PHONG;
const UseVertexNormals = true;
function EdgeInterpolate(y0, v0, y1, v1, y2, v2) {
let v01 = Interpolate(y0, v0, y1, v1);
let v12 = Interpolate(y1, v1, y2, v2);
let v02 = Interpolate(y0, v0, y2, v2);
v01.pop();
let v012 = v01.concat(v12);
return [v02, v012];
}
function RenderTriangle(triangle, vertices, projected, camera, lights, orientation, specular) {
// Compute triangle normal. Use the unsorted vertices, otherwise the winding of the points may change.
let normal = ComputeTriangleNormal(vertices[triangle.indexes[0]], vertices[triangle.indexes[1]], vertices[triangle.indexes[2]]);
// Backface culling.
let vertex_to_camera = vertices[triangle.indexes[0]].mul(-1); // Should be Subtract(camera.position, vertices[triangle.indexes[0]])
if (vertex_to_camera.dot(normal) <= 0) {
return;
}
// Sort by projected point Y.
let indexes = SortedVertexIndexes(triangle.indexes, projected);
let [i0, i1, i2] = indexes;
let [v0, v1, v2] = [ vertices[triangle.indexes[i0]], vertices[triangle.indexes[i1]], vertices[triangle.indexes[i2]] ];
// Get attribute values (X, 1/Z) at the vertices.
let p0 = projected[triangle.indexes[i0]];
let p1 = projected[triangle.indexes[i1]];
let p2 = projected[triangle.indexes[i2]];
// Compute attribute values at the edges.
let [x02, x012] = EdgeInterpolate(p0.y, p0.x, p1.y, p1.x, p2.y, p2.x);
let [iz02, iz012] = EdgeInterpolate(p0.y, 1.0/v0.z, p1.y, 1.0/v1.z, p2.y, 1.0/v2.z);
if (UseVertexNormals) {
let transform = MultiplyMM4(Transposed(camera.orientation), orientation);
var normal0 = MultiplyMV(transform, new Vertex4(triangle.normals[i0]));
var normal1 = MultiplyMV(transform, new Vertex4(triangle.normals[i1]));
var normal2 = MultiplyMV(transform, new Vertex4(triangle.normals[i2]));
} else {
var normal0 = normal;
var normal1 = normal;
var normal2 = normal;
}
let intensity;
if (ShadingModel == SM_FLAT) {
// Flat shading: compute lighting for the entire triangle.
let center = Vertex((v0.x + v1.x + v2.x)/3.0, (v0.y + v1.y + v2.y)/3.0, (v0.z + v1.z + v2.z)/3.0);
intensity = ComputeIllumination(center, normal0, camera, lights, specular);
} else if (ShadingModel == SM_GOURAUD) {
// Gouraud shading: compute lighting at the vertices, and interpolate.
let i0 = ComputeIllumination(v0, normal0, camera, lights, specular);
let i1 = ComputeIllumination(v1, normal1, camera, lights, specular);
let i2 = ComputeIllumination(v2, normal2, camera, lights, specular);
var [i02, i012] = EdgeInterpolate(p0.y, i0, p1.y, i1, p2.y, i2);
} else if (ShadingModel == SM_PHONG) {
// Phong shading: interpolate normal vectors.
var [nx02, nx012] = EdgeInterpolate(p0.y, normal0.x, p1.y, normal1.x, p2.y, normal2.x);
var [ny02, ny012] = EdgeInterpolate(p0.y, normal0.y, p1.y, normal1.y, p2.y, normal2.y);
var [nz02, nz012] = EdgeInterpolate(p0.y, normal0.z, p1.y, normal1.z, p2.y, normal2.z);
}
// Determine which is left and which is right.
let m = (x02.length/2) | 0;
if (x02[m] < x012[m]) {
var [x_left, x_right] = [x02, x012];
var [iz_left, iz_right] = [iz02, iz012];
var [i_left, i_right] = [i02, i012];
var [nx_left, nx_right] = [nx02, nx012];
var [ny_left, ny_right] = [ny02, ny012];
var [nz_left, nz_right] = [nz02, nz012];
} else {
var [x_left, x_right] = [x012, x02];
var [iz_left, iz_right] = [iz012, iz02];
var [i_left, i_right] = [i012, i02];
var [nx_left, nx_right] = [nx012, nx02];
var [ny_left, ny_right] = [ny012, ny02];
var [nz_left, nz_right] = [nz012, nz02];
}
// Draw horizontal segments.
for (let y = p0.y; y <= p2.y; y++) {
let [xl, xr] = [x_left[y - p0.y] | 0, x_right[y - p0.y] | 0];
// Interpolate attributes for this scanline.
let [zl, zr] = [iz_left[y - p0.y], iz_right[y - p0.y]];
let zscan = Interpolate(xl, zl, xr, zr);
let iscan, nxscan, nyscan, nzscan;
if (ShadingModel == SM_GOURAUD) {
let [il, ir] = [i_left[y - p0.y], i_right[y - p0.y]];
iscan = Interpolate(xl, il, xr, ir);
} else if (ShadingModel == SM_PHONG) {
let [nxl, nxr] = [nx_left[y - p0.y], nx_right[y - p0.y]];
let [nyl, nyr] = [ny_left[y - p0.y], ny_right[y - p0.y]];
let [nzl, nzr] = [nz_left[y - p0.y], nz_right[y - p0.y]];
nxscan = Interpolate(xl, nxl, xr, nxr);
nyscan = Interpolate(xl, nyl, xr, nyr);
nzscan = Interpolate(xl, nzl, xr, nzr);
}
for (let x = xl; x <= xr; x++) {
let inv_z = zscan[x - xl];
if (UpdateDepthBufferIfCloser(x, y, inv_z)) {
if (ShadingModel == SM_FLAT) {
// Just use the per-triangle intensity.
} else if (ShadingModel == SM_GOURAUD) {
intensity = iscan[x-xl];
} else if (ShadingModel == SM_PHONG) {
let vertex = UnProjectVertex(x, y, inv_z);
let normal = Vertex(nxscan[x - xl], nyscan[x - xl], nzscan[x - xl]);
intensity = ComputeIllumination(vertex, normal, camera, lights, specular);
}
PutPixel(x, y, triangle.color.mul(intensity));
}
}
}
}
// Clips a triangle against a plane. Adds output to triangles and vertices.
function ClipTriangle(triangle, plane, triangles, vertices) {
let v0 = vertices[triangle.indexes[0]];
let v1 = vertices[triangle.indexes[1]];
let v2 = vertices[triangle.indexes[2]];
let in0 = plane.normal.dot(v0) + plane.distance > 0;
let in1 = plane.normal.dot(v1) + plane.distance > 0;
let in2 = plane.normal.dot(v2) + plane.distance > 0;
let in_count = in0 + in1 + in2;
if (in_count == 0) {
// Nothing to do - the triangle is fully clipped out.
} else if (in_count == 3) {
// The triangle is fully in front of the plane.
triangles.push(triangle);
} else if (in_count == 1) {
// The triangle has one vertex in. Output is one clipped triangle.
} else if (in_count == 2) {
// The triangle has two vertices in. Output is two clipped triangles.
}
}
function TransformAndClip(clipping_planes, model, scale, transform) {
// Transform the bounding sphere, and attempt early discard.
let center = MultiplyMV(transform, new Vertex4(model.bounds_center));
let radius = model.bounds_radius*scale;
for (let p = 0; p < clipping_planes.length; p++) {
let distance = clipping_planes[p].normal.dot(center) + clipping_planes[p].distance;
if (distance < -radius) {
return null;
}
}
// Apply modelview transform.
let vertices = [];
for (let i = 0; i < model.vertices.length; i++) {
vertices.push(MultiplyMV(transform, new Vertex4(model.vertices[i])));
}
// Clip the entire model against each successive plane.
let triangles = model.triangles.slice();
for (let p = 0; p < clipping_planes.length; p++) {
let new_triangles = []
for (let i = 0; i < triangles.length; i++) {
ClipTriangle(triangles[i], clipping_planes[p], new_triangles, vertices);
}
triangles = new_triangles;
}
return Model(vertices, triangles, center, model.bounds_radius);
}
function RenderModel(model, camera, lights, orientation, specular) {
let projected = [];
for (let i = 0; i < model.vertices.length; i++) {
projected.push(ProjectVertex(new Vertex4(model.vertices[i])));
}
for (let i = 0; i < model.triangles.length; i++) {
RenderTriangle(model.triangles[i], model.vertices, projected, camera, lights, orientation, specular);
}
}
function RenderScene(camera, instances, lights) {
let cameraMatrix = MultiplyMM4(Transposed(camera.orientation), MakeTranslationMatrix(camera.position.mul(-1)));
for (let i = 0; i < instances.length; i++) {
let transform = MultiplyMM4(cameraMatrix, instances[i].transform);
let clipped = TransformAndClip(camera.clipping_planes, instances[i].model, instances[i].scale, transform);
if (clipped != null) {
RenderModel(clipped, camera, lights, instances[i].orientation, instances[i].specular);
}
}
}
// ----- Sphere model generator -----
function GenerateSphere(divs, color) {
let vertices = [];
let triangles = [];
let delta_angle = 2.0*Math.PI / divs;
// Generate vertices and normals.
for (let d = 0; d < divs + 1; d++) {
let y = (2.0 / divs) * (d - divs/2);
let radius = Math.sqrt(1.0 - y*y);
for (let i = 0; i < divs; i++) {
let vertex = new Vertex(radius*Math.cos(i*delta_angle), y, radius*Math.sin(i*delta_angle));
vertices.push(vertex);
}
}
// Generate triangles.
for (let d = 0; d < divs; d++) {
for (let i = 0; i < divs - 1; i++) {
let i0 = d*divs + i;
triangles.push(Triangle([i0, i0+divs+1, i0+1], color, [vertices[i0], vertices[i0+divs+1], vertices[i0+1]]));
triangles.push(Triangle([i0, i0+divs, i0+divs+1], color, [vertices[i0], vertices[i0+divs], vertices[i0+divs+1]]));
}
}
return new Model(vertices, triangles, new Vertex(0, 0, 0), 1.0);
}
// ----- Floor "plane" (because of approximate clipping, must fit in frustum -----
let size = 50;
const vertices = [
new Vertex(-(size - 1), 0, size),
new Vertex( size - 1, 0, size),
new Vertex( 0.999, 0, 1.01),
new Vertex( -0.999, 0, 1.01),
];
const RED = new Color(255, 0, 0);
const GREEN = new Color(0, 255, 0);
const BLUE = new Color(0, 0, 255);
const YELLOW = new Color(255, 255, 0);
const PURPLE = new Color(255, 0, 255);
const CYAN = new Color(0, 255, 255);
const triangles = [
new Triangle([0, 1, 2], YELLOW, [new Vertex(0, 1, 0), new Vertex(0, 1, 0), new Vertex(0, 1, 0)]),
new Triangle([0, 2, 3], YELLOW, [new Vertex(0, 1, 0), new Vertex(0, 1, 0), new Vertex(0, 1, 0)]),
];
const floor = new Model(vertices, triangles, new Vertex(0, 0, 1000), 1);
// ----------
const green_sphere = GenerateSphere(15, GREEN);
const red_sphere = GenerateSphere(15, RED);
const blue_sphere = GenerateSphere(15, BLUE);
const instances = [
new Instance(red_sphere, new Vertex( 0, -1, 3), Identity4x4, 1, 500),
new Instance(green_sphere, new Vertex(-2, 0, 4), MakeOYRotationMatrix(180), 1, 10),
new Instance(blue_sphere, new Vertex( 2, 0, 4), Identity4x4, 1, 500),
new Instance(floor, new Vertex( 0, -1, 0), Identity4x4),
];
const camera = new Camera(new Vertex(0, 0, 0), Identity4x4);
let s2 = 1.0 / Math.sqrt(2);
camera.clipping_planes = [
new Plane(new Vertex( 0, 0, 1), -1), // Near
new Plane(new Vertex( s2, 0, s2), 0), // Left
new Plane(new Vertex(-s2, 0, s2), 0), // Right
new Plane(new Vertex( 0, -s2, s2), 0), // Top
new Plane(new Vertex( 0, s2, s2), 0), // Bottom
];
const lights = [
new Light(LT_AMBIENT, 0.2),
new Light(LT_POINT, 0.6, new Vertex(2, 1, 0)),
new Light(LT_DIRECTIONAL, 0.2, new Vertex(1, 4, 4)),
];
function Render() {
RenderScene(camera, instances, lights);
UpdateCanvas();
}
Render();
</script>