可视化:https://www.cs.usfca.edu/~galles/visualization/AVLtree.html
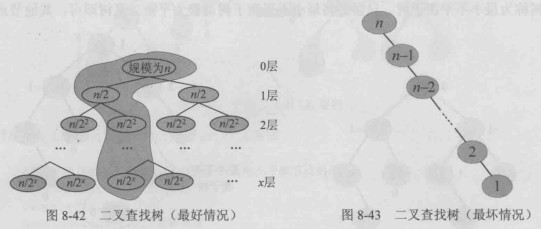
二叉查找树的查找、插入、删除的时间复杂度均为 O(logn),但这个是在期望的情况下,最好情况和 最坏情况差别较大。

平衡二叉查找树(Balanced Binary Search Tree,BBST),简称平衡二叉树,由苏联数学家 Adelson-Velskii和Landis提出,所以又称 AVL树。
具有一下性质的平衡二叉树:
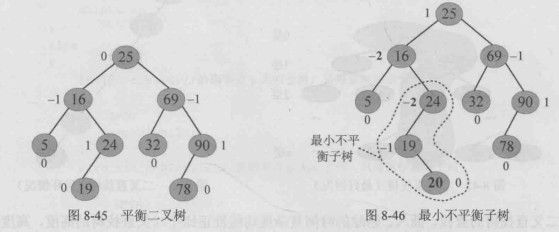
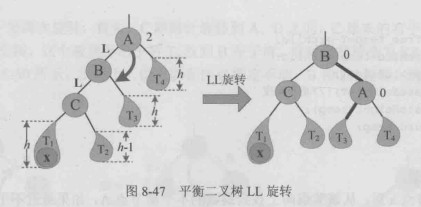
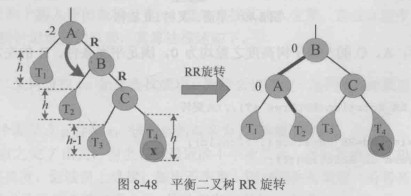
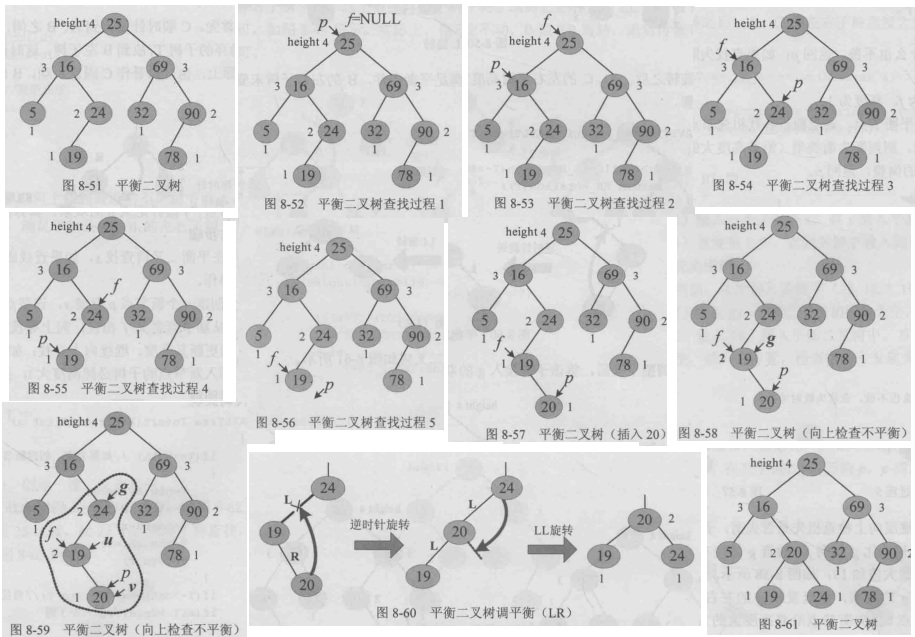
插入元素20
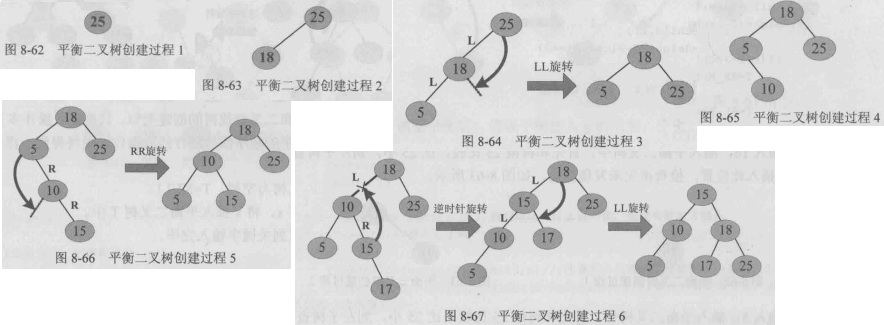
平衡二叉树的创建和二叉查找树的创建类似,只是插入操作多了调平衡而已,可以从空树开始,按照输入关键字的顺序 依次进行插入操作,最终得到一棵平衡二叉树。
例如,一棵二叉平衡树,删除16
16为叶子,直接删除即可
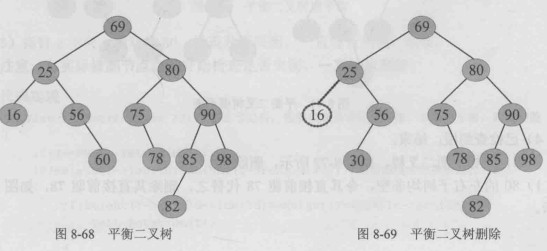
删除后25失衡,g、u、v记录失衡三代节点(从失衡节点沿着高度大的子树向下找三代)
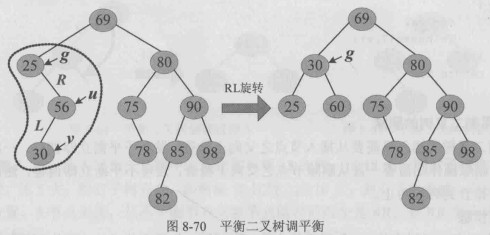
继续向上检查
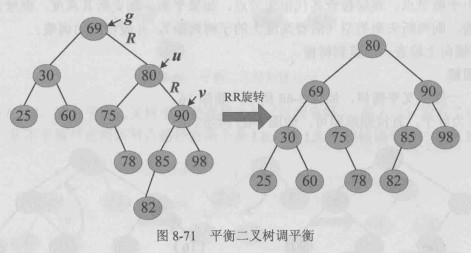
例如,一棵平衡二叉树,删除80
80的左右子树均非空,令其直接前驱78代替之,删除其直接前驱78
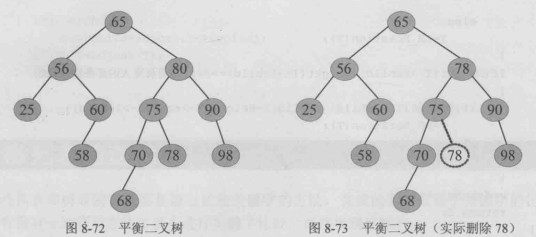
g指向实际被删除节点78之父75,检查是否失衡,75节点失衡,用 g,u,v记录失衡三代节点,判断为LL,进行LL旋转。
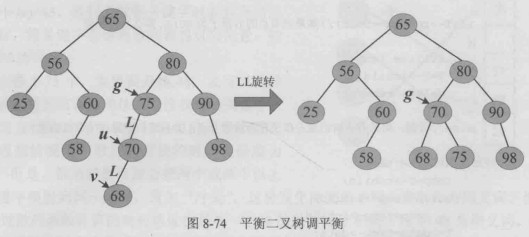
g指向g的双亲80,检查是否失衡,一直检查到根,结束。
注意:从实际被删节点之父开始检查是否失衡,一直检查到根。
#include <stdio.h>
#include <stdlib.h>
/* ================= AVL 节点定义 ================= */
typedef struct AVLNode {
int key;
int height;
struct AVLNode *left;
struct AVLNode *right;
} AVLNode;
/* ================= 工具函数 ================= */
// 获取最大值
static int max(int a, int b) {
return a > b ? a : b;
}
// 获取节点高度
static int height(AVLNode *node) {
return node ? node->height : 0;
}
// 创建新节点
AVLNode *avl_create_node(int key) {
AVLNode *node = (AVLNode *)malloc(sizeof(AVLNode));
if (!node) {
perror("malloc failed");
exit(1);
}
node->key = key;
node->height = 1;
node->left = node->right = NULL;
return node;
}
// 获取平衡因子
static int get_balance(AVLNode *node) {
if (!node) return 0;
return height(node->left) - height(node->right);
}
/* ================= 旋转操作 ================= */
// LL 旋转(右旋)
static AVLNode *rotate_right(AVLNode *y) {
AVLNode *x = y->left;
AVLNode *T2 = x->right;
x->right = y;
y->left = T2;
y->height = max(height(y->left), height(y->right)) + 1;
x->height = max(height(x->left), height(x->right)) + 1;
return x;
}
// RR 旋转(左旋)
static AVLNode *rotate_left(AVLNode *x) {
AVLNode *y = x->right;
AVLNode *T2 = y->left;
y->left = x;
x->right = T2;
x->height = max(height(x->left), height(x->right)) + 1;
y->height = max(height(y->left), height(y->right)) + 1;
return y;
}
/* ================= 插入 ================= */
AVLNode *avl_insert(AVLNode *node, int key) {
if (!node)
return avl_create_node(key);
if (key < node->key)
node->left = avl_insert(node->left, key);
else if (key > node->key)
node->right = avl_insert(node->right, key);
else
return node; // 不允许重复键
node->height = 1 + max(height(node->left), height(node->right));
int balance = get_balance(node);
// LL
if (balance > 1 && key < node->left->key)
return rotate_right(node);
// RR
if (balance < -1 && key > node->right->key)
return rotate_left(node);
// LR
if (balance > 1 && key > node->left->key) {
node->left = rotate_left(node->left);
return rotate_right(node);
}
// RL
if (balance < -1 && key < node->right->key) {
node->right = rotate_right(node->right);
return rotate_left(node);
}
return node;
}
/* ================= 删除 ================= */
// 找最小节点
static AVLNode *min_value_node(AVLNode *node) {
AVLNode *current = node;
while (current->left)
current = current->left;
return current;
}
AVLNode *avl_delete(AVLNode *root, int key) {
if (!root)
return root;
if (key < root->key)
root->left = avl_delete(root->left, key);
else if (key > root->key)
root->right = avl_delete(root->right, key);
else {
// 一个或零个子节点
if (!root->left || !root->right) {
AVLNode *temp = root->left ? root->left : root->right;
if (!temp) {
temp = root;
root = NULL;
} else {
*root = *temp;
}
free(temp);
} else {
// 两个子节点
AVLNode *temp = min_value_node(root->right);
root->key = temp->key;
root->right = avl_delete(root->right, temp->key);
}
}
if (!root)
return root;
root->height = 1 + max(height(root->left), height(root->right));
int balance = get_balance(root);
// LL
if (balance > 1 && get_balance(root->left) >= 0)
return rotate_right(root);
// LR
if (balance > 1 && get_balance(root->left) < 0) {
root->left = rotate_left(root->left);
return rotate_right(root);
}
// RR
if (balance < -1 && get_balance(root->right) <= 0)
return rotate_left(root);
// RL
if (balance < -1 && get_balance(root->right) > 0) {
root->right = rotate_right(root->right);
return rotate_left(root);
}
return root;
}
/* ================= 遍历 ================= */
void avl_inorder(AVLNode *root) {
if (!root) return;
avl_inorder(root->left);
printf("%d ", root->key);
avl_inorder(root->right);
}
/* ================= 测试主函数 ================= */
int main(void) {
AVLNode *root = NULL;
int values[] = {10, 20, 30, 40, 50, 25};
int n = sizeof(values) / sizeof(values[0]);
for (int i = 0; i < n; i++)
root = avl_insert(root, values[i]);
printf("AVL 中序遍历(插入后):\n");
avl_inorder(root);
printf("\n");
root = avl_delete(root, 40);
printf("AVL 中序遍历(删除 40 后):\n");
avl_inorder(root);
printf("\n");
return 0;
}