可视化:https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html
m 阶 B+ 树(B+ Tree of order ( m ))是一种多路平衡查找树,广泛应用于数据库索引与文件系统中。设 ( m ) 为树的阶,则每个内部节点最多包含 ( m ) 个子节点,并至多存放 ( m-1 ) 个关键字。除根节点外,任一内部节点的子节点数满足
相应的关键字数满足
B+ 树的所有实际数据记录仅存储在叶子节点中,内部节点只用于索引与路径导航。所有叶子节点位于同一层,并按照关键字大小顺序通过指针连接成有序链表,从而支持高效的顺序访问与范围查询。
由于 B+ 树具有较高的分支因子,其整体高度较低,在查找、插入和删除操作中均可保持
的时间复杂度,尤其适合基于磁盘或其他外存介质的存储结构。
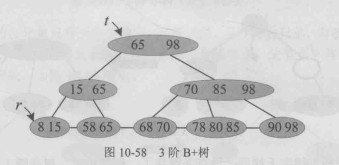
例如,一棵3阶B+树,其内部节点的子树个数
2<=k<=3,关键字个数也是2<=n<=3,一般有两个指针,一个指向树根,一个指向倒数第二层关键字最小的节点。

最后一层内部节点就是一个分块的顺序链表,父节点记录了子节点的最大关键字。
在 m 阶 B+ 树中,节点内部通常包含两类指针:t 指针(tree pointer) 与 r 指针(record pointer),分别用于索引导航与数据访问。
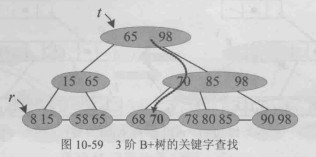
t 指针查找是指在查找过程中,根据内部节点中关键字的比较结果,沿着 t 指针在树结构中自顶向下逐层下降,直至到达某个叶子节点。该过程仅涉及索引节点之间的跳转,其查找路径长度等于树的高度 ( h ),时间复杂度为
r 指针查找发生在到达叶子节点之后。叶子节点中的关键字与 r 指针一一对应,r 指针直接指向实际的数据记录或记录所在的物理地址。通过 r 指针即可完成对目标数据的精确访问,不再涉及树结构的继续遍历。
在实际应用中,B+ 树的查找过程通常表现为:先通过 t 指针完成索引定位,再通过 r 指针完成数据访问。这种指针分离的设计减少了内部节点的存储负担,提高了索引节点的扇出率,从而降低了整体查找过程中的磁盘 I/O 次数。
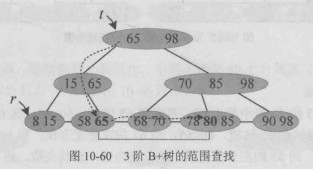
B+ 树不仅支持基于单个关键字的精确查找,还天然支持范围查找操作。例如,在给定关键字区间 ([a, b]) 时,首先通过索引查找定位到包含关键字 (a) 的叶子节点;随后沿叶子节点之间的有序链表顺序遍历,依次访问关键字不小于 (a) 且不大于 (b) 的所有记录,直至遇到大于 (b) 的关键字为止。
由于所有叶子节点按照关键字大小顺序相互连接,范围查找过程中无需重复回溯或重新进行树搜索,其整体时间复杂度可表示为
其中
为定位起始关键字 (a) 所需的查找代价,( k ) 为区间 ([a, b]) 内满足条件的关键字数量。
这种基于顺序链表的范围访问机制,使 B+ 树在区间查询、排序扫描等场景中具有显著优势。
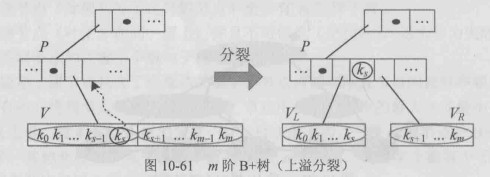
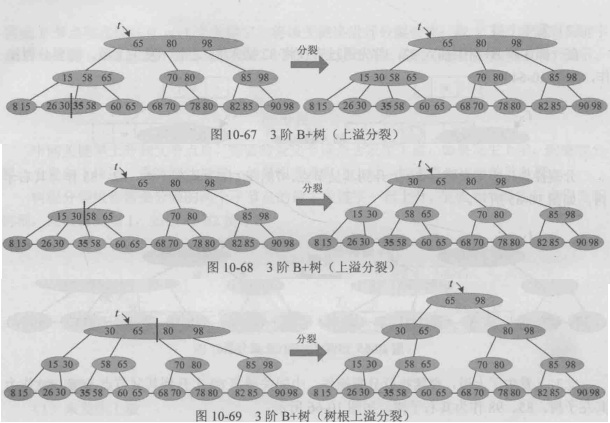
m阶B+树,仅在最后一层节点插入,因为除了最后一层节点,其他非终端节点都表示索引。 又因为m阶B+树的关键字个数要求不超过m,如果插入后节点的关键字个数超过m, 则发生上溢,需要分裂操作,只不过分裂时,和B-树的分裂不同,上升到父节点的关键字,子节点中仍然保留。
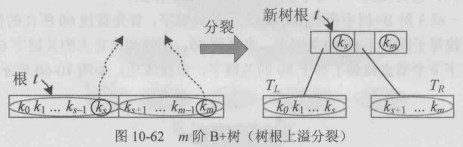
未发生上溢:
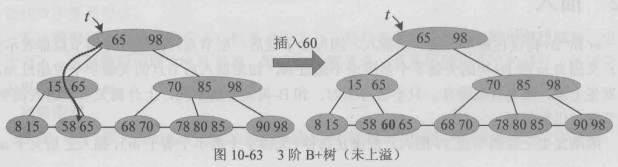
发生上溢
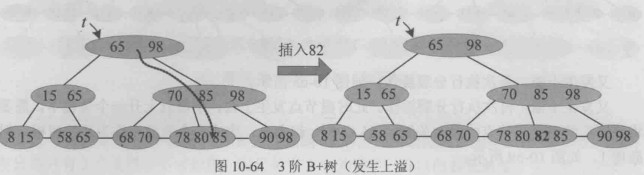
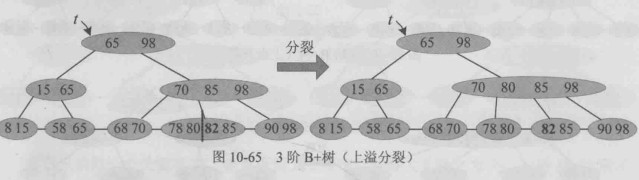

发生上溢,树根分裂:
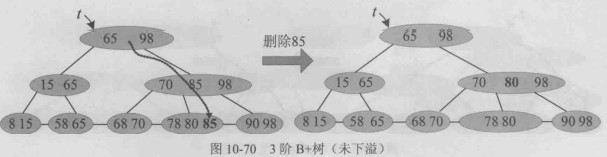
m阶B+树的删除只在最后一层进行,首先通过查找确定待删除关键字的位置,删除之,然后判断该节点是否发生下溢,还要判断是否需要更新父节点的关键字,
如果关键字个数小于 ceil(m/2)
则发生下溢,如果发生下溢,则需要像B-树那样左借,右借或合并以解除下溢。
接触下溢时要特别注意父节点中的最大关键字更新。
未发生下溢:
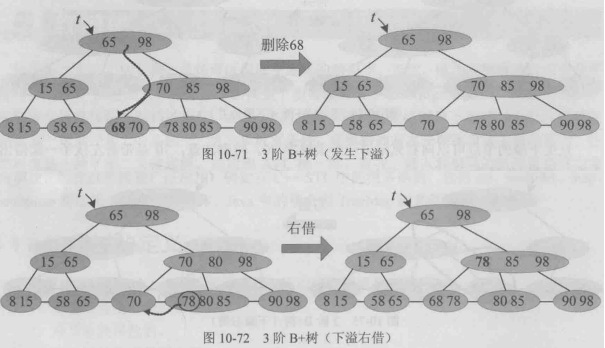
发生下溢,右借,左边没法借
发生下溢(合并):
在一棵3阶B+树中删除8,首先查找到8的位置,将其删除,删除后该节点发生下溢,其没有左兄弟, 右兄弟只有2个关键字不可以借,可以和右兄弟合并。
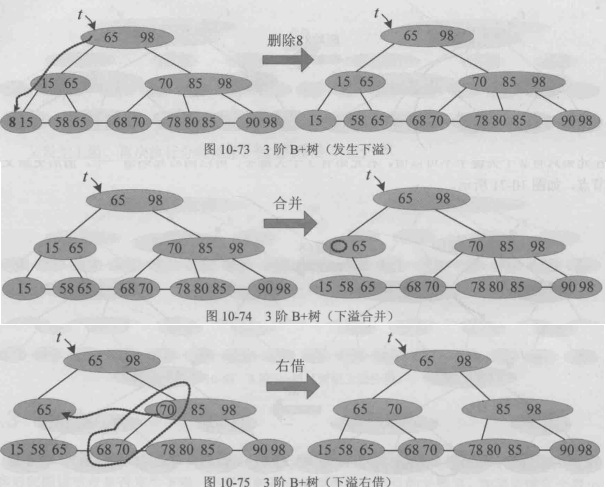
与右兄弟合并后,需删除父节点中该位置的关键字15,删除后再次发生下溢。
发生下溢出的节点可以向右兄弟借一个关键字70,特别注意,70是带着左孩子一起借出去的。
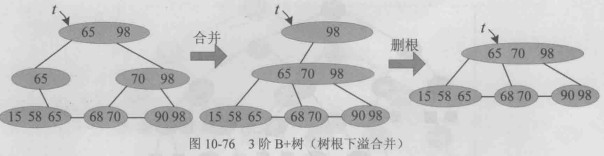
发生下溢(树根):
如果发生下溢的节点的左右兄弟都不可以借,则和兄弟的执行合并操作,合并后删除其父节点所在位置的关键字,删除后,根节点发生下溢, 直接删除根节点即可,树高减1。
含有n个关键字的m阶B+树,查找、插入和删除操作的时间复杂度均为树的高度