
可视化:https://www.cs.usfca.edu/~galles/visualization/BTree.html
要注意:口语里说的「B 树」,大多数情况下指的是「B+ 树」,但严格来说二者是不同的数据结构。
| 系统 | 实际使用 |
|---|---|
| MySQL InnoDB | B+ 树 |
| MySQL MyISAM | B+ 树 |
| PostgreSQL | B+ 树 |
| SQLite | B+ 树 |
| NTFS / ext4 | B+ 树 |
| Redis(有序结构) | 思想接近 B+ 树 |
二叉搜索树的搜索效率和树高成正比关系,通过减少二叉搜索树的高度,可以提高搜索效率。
二叉平衡树可以减少树高,但是仍然不够彻底,因为每个节点只含有一个关键字,树高仍然为
O(logn),能否继续压缩树高,使其更加扁平化呢?
如果一个节点不限于存储一个关键字,就可以包含多个关键字和多个子树,既保持二叉搜索树的特性,又具有平衡性,这样的搜索树称为 多路平衡搜索树。
平衡二叉搜索树比普通的二叉搜索树高低,而多路平衡搜索树的树高更低,更加扁平化,搜索的效率更高。

那么是不是越扁平就越好?再压缩下去,就变成一个包含所有节点的树根了。
多路平衡搜索树 主要用于大规模数据的分级存储搜索,将内存的“高速度”和外存的“大容量”结合起来,提高搜索效率,内存的访问速度是很快的,而外存的访问速度则慢 5-6 个数量级,数据规模巨大时,无法全部放入内存, 数据全集往往放在外存种,如果频繁地访问外存,则搜索地效率降低,如何减少外存操作呢?
外存访问时,访问一个数据和访问一段连续存储的数据,时间差别不大,因此可以用“大节点”代替多个单个节点,一个“大节点”包含多个连续存储的数据,它们作为一个整体,进行一次外存访问,将这个“大节点”调入内存后,再进行多次内存操作,例如顺序查找或折半查找,与外存访问相比,内存操作的成本很小。
一个“大节点”到底包含多少个数据元素合适呢?主要取决于不同外存的批量访问特性。例如,可以根据磁盘扇区的容量和数据元素的大小计算出一个“大节点”包含的数据元素个数。若一个“大节点”包含 255 个数据元素,那么每次查找 1G 个数据元素需要 4~5 次外存访问,而如果使用平衡二叉搜索树(AVL 树),则每次查找需要 30 次外存访问。
ceil(m/2)
棵子树根节点至少有一个关键字和两棵子树,其他非终端节点关键字个数范围为
[ceil(m/2)-1, m-1],子树个数范围为
[ceil(m/2), m]
3阶B-树,其内部节点的子树个数 2<=k<=3 所以又称为
2-3树,每个节点有 1-2个关键字,2-3棵子树,所有的叶子都在最后一层。
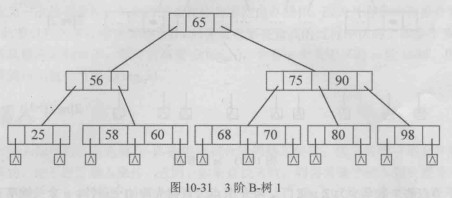
B-树具有
平衡、有序、多路的特点,在B-树种,所有的叶子节点都在最后一层,因此左右子树的高差为0,体现了平衡的特性,B-树具有中序有序的特性
左子树<根<右子树。多路是指可以有多个分支,m阶B-树种的节点最多可以有m个分支,所以称为m路平衡搜索树。
首先要看每层至少有多少个节点,因为节点越少,高度越大。根据定义,根节点至少有两棵子树,那么第二层至少有
2 个节点;除了根之外,每个非叶子节点至少有 ⌈m/2⌉
棵子树,每个子树对应一个节点,因此第三层至少有 2⌈m/2⌉
个节点……依次类推,第 h+1 层至少有 2⌈m/2⌉^(h−1) 个节点。
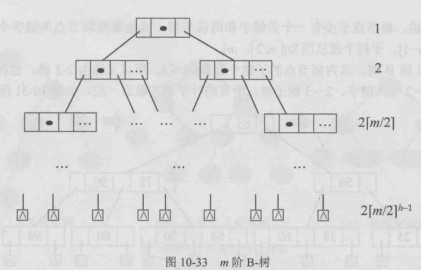
叶子节点的个数至少为
叶子节点为查找失败的空指针,(n) 个关键字有 (n+1) 种查找失败的情况,因此有:
由此可得树高 (h) 的上界:
一棵含有 (n) 个关键字的 (m) 阶 B 树,其最大高度为
后续对 B 树的查找、插入、删除等基本操作 的时间复杂度分析,均可以利用这一结论。
插入时,从根节点开始按关键字大小向下查找,最终定位到一个叶子节点,并将新关键字按有序顺序插入到该叶子节点中。如果插入后该节点中的关键字个数不超过 (m-1),则插入过程结束。
当插入后某个节点中的关键字个数达到 (m) 时,节点发生上溢。此时需要对该节点进行分裂:选取中间关键字(通常为第
个关键字)作为提升关键字,将其上移插入到父节点中;原节点被分裂为左右两个节点,左节点保留中间关键字之前的关键字,右节点保留中间关键字之后的关键字,相应的子树指针也按顺序分配。
若父节点在插入提升关键字后仍满足 B-树的节点容量约束,则分裂过程结束;否则父节点同样发生上溢,需要按照相同的规则继续向上分裂。该过程可能沿着插入路径一直向上传播。
当根节点发生上溢时,需对根节点进行分裂,并将提升的中间关键字作为新的根节点,原根节点分裂得到的两个节点成为新根的两个子节点,此时 B-树的高度增加 1。整个插入与上溢处理过程保证了 B-树始终保持平衡,其高度为
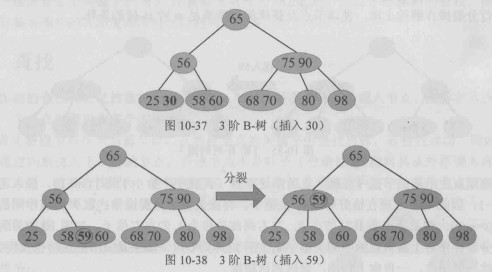
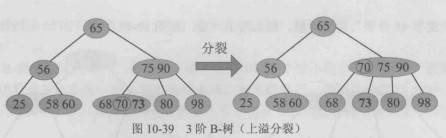
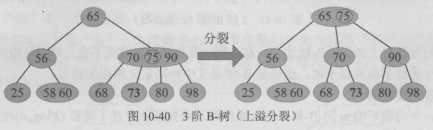
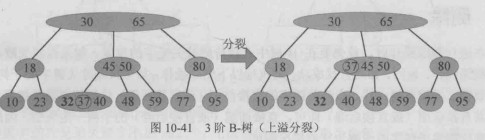
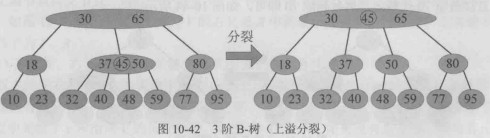
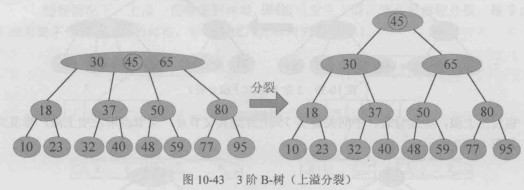
只有树根发生上溢时,B-树才会长高一层,其他情况,树高不变,树根分裂时,新的树根只有一个关键字和两棵子树,这也是B-树定义中特殊定义树根的原因。
含有 (n) 个关键字的 (m) 阶 B-树,插入操作除了查找插入位置(需要
的时间)之外,如果发生上溢,还需要分裂操作。分裂操作不会超过树的高度
,因此插入操作的时间复杂度为
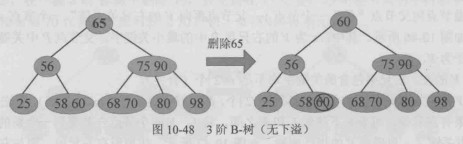
删除关键字时,首先在 B-树中定位该关键字。若关键字位于内部节点,通常用其前驱或后继关键字替换,再转化为在叶子节点中删除。删除后,如果节点中的关键字个数仍不少于 (m/2),则满足 B-树约束,删除过程结束。
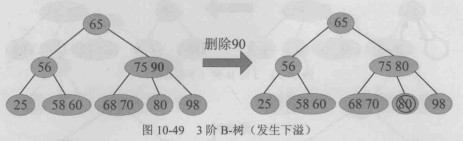
当删除后某节点中的关键字个数 小于
时,节点发生下溢(underflow),需要通过向兄弟节点借关键字或进行节点合并来恢复 B-树的性质。
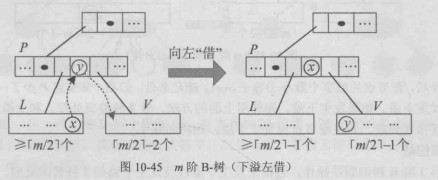
若该节点的左兄弟存在,且左兄弟中的关键字个数 大于
,则可以进行左借:将父节点中分隔当前节点与左兄弟的关键字下移到当前节点的最左侧,同时将左兄弟中最大的关键字上移替换父节点中的分隔关键字;若为非叶子节点,还需相应移动最右侧子树指针。左兄弟关键字数减少 1,当前节点关键字数增加 1,下溢被消除。
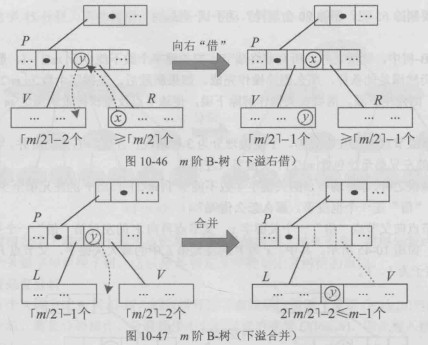
若左兄弟无法借用,而右兄弟存在且关键字个数大于
,则进行右借:将父节点中分隔当前节点与右兄弟的关键字下移到当前节点的最右侧,同时将右兄弟中最小的关键字上移替换父节点中的分隔关键字;相应的子树指针也随之调整。右兄弟关键字数减少 1,当前节点关键字数增加 1。
若左右兄弟都无法借用(即它们的关键字个数均为最小值),则必须进行合并:将父节点中的分隔关键字下移,与当前节点及其某一兄弟节点(通常选择左或右之一)合并成一个节点。合并后节点的关键字个数不超过 (m-1),但父节点的关键字数减少 1,可能导致父节点发生下溢。
如果父节点发生下溢,则需对父节点重复上述“借或合并”的处理过程,可能一路向上传播。当根节点关键字数减为 0 时,若其仍有子节点,则将唯一的子节点提升为新的根,B-树高度减少 1。整个删除及下溢处理过程的时间复杂度为
无下溢情况:
下溢左借情况:
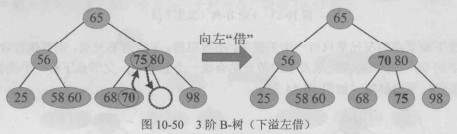
下溢右借情况:
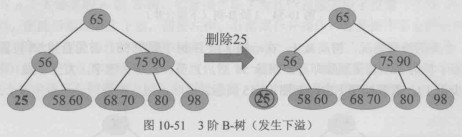
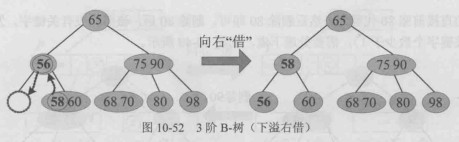
下溢合并情况:
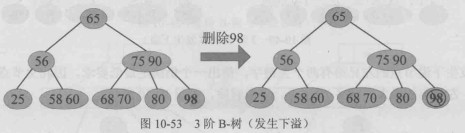
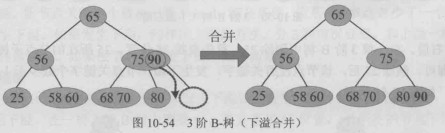
下溢合并的特殊情况,树高减1:
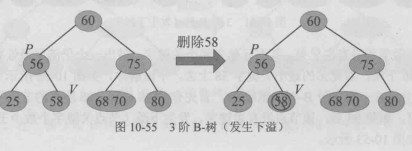
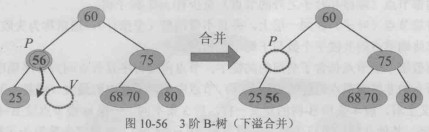
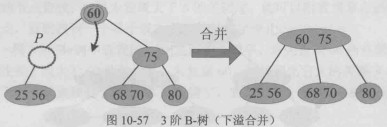
含有 (n) 个关键字的 (m) 阶 B-树,在执行删除操作时,首先需要在树中查找待删除的关键字。B-树的高度为
,因此查找过程的时间复杂度为
删除关键字后,若节点仍满足最少关键字数的约束,则操作结束;否则会发生下溢,需要通过向兄弟节点借关键字或进行节点合并来恢复 B-树的性质。一次借或合并操作只涉及常数个节点,但下溢处理可能沿着删除路径向上递归传播,其次数不会超过树的高度,即
因此,删除操作的总体时间复杂度为
该复杂度同时适用于最坏情况和平均情况,表明 B-树在大量数据的动态维护中具有稳定而高效的性能。
含有十亿个节点的3阶B-树的高度仅在19-30之间,最多访问30个节点就能够在10亿个键中进行任何查找、插入、删除操作,这个速度是相当惊人的。
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
/*
* B 树的最小度数 t
*
* 性质(CLRS 定义):
* 1. 每个节点最多有 2t-1 个关键字
* 2. 每个非根节点至少有 t-1 个关键字
* 3. 每个内部节点有 n+1 个孩子(n 为关键字数)
*
* 这里 T = 3
* ⇒ 每个节点最多 5 个 key,最少 2 个 key(非根)
*/
#define T 3
/*
* B 树节点结构
*/
typedef struct BTreeNode {
int keys[2 * T - 1]; // 关键字数组(有序)
struct BTreeNode* child[2 * T]; // 子节点指针数组
int n; // 当前节点中 key 的数量
bool leaf; // 是否为叶子节点
} BTreeNode;
/*
* 创建一个新节点
* leaf = true 表示叶子节点
* leaf = false 表示内部节点
*/
BTreeNode* btree_create_node(bool leaf) {
BTreeNode* node = (BTreeNode*)malloc(sizeof(BTreeNode));
node->leaf = leaf;
node->n = 0;
// 初始化子指针
for (int i = 0; i < 2 * T; i++)
node->child[i] = NULL;
return node;
}
/*
* 创建一棵空 B 树
* 初始只有一个叶子根节点
*/
BTreeNode* btree_create() {
return btree_create_node(true);
}
/*
* 在 B 树中查找 key
*
* 算法:
* 1. 在当前节点中线性查找第一个 >= k 的 key
* 2. 若命中直接返回
* 3. 若是叶子则失败
* 4. 否则递归进入对应子树
*/
BTreeNode* btree_search(BTreeNode* x, int k) {
int i = 0;
// 找到第一个 >= k 的 key
while (i < x->n && k > x->keys[i])
i++;
// 命中
if (i < x->n && k == x->keys[i])
return x;
// 叶子节点仍未找到
if (x->leaf)
return NULL;
// 递归下降
return btree_search(x->child[i], k);
}
/*
* 分裂满子节点(核心操作)
*
* x : 父节点
* i : 要分裂的子节点下标
*
* 过程:
* 1. y = x->child[i](满节点)
* 2. 创建新节点 z
* 3. y 的后半部分 key / child 移到 z
* 4. y 的中间 key 上升到父节点 x
* 5. x 的 child / key 右移,插入 z
*/
void btree_split_child(BTreeNode* x, int i) {
BTreeNode* y = x->child[i]; // 原满节点
BTreeNode* z = btree_create_node(y->leaf); // 新节点
// z 拿走 y 后半部分的 key
z->n = T - 1;
for (int j = 0; j < T - 1; j++)
z->keys[j] = y->keys[j + T];
// 如果不是叶子,子指针也要转移
if (!y->leaf) {
for (int j = 0; j < T; j++)
z->child[j] = y->child[j + T];
}
// y 只保留前半部分
y->n = T - 1;
// 父节点 child 指针右移
for (int j = x->n; j >= i + 1; j--)
x->child[j + 1] = x->child[j];
x->child[i + 1] = z;
// 父节点 key 右移
for (int j = x->n - 1; j >= i; j--)
x->keys[j + 1] = x->keys[j];
// y 的中间 key 上升
x->keys[i] = y->keys[T - 1];
x->n++;
}
/*
* 向非满节点插入 key
*
* 保证调用该函数时:
* x->n < 2T - 1
*/
void btree_insert_nonfull(BTreeNode* x, int k) {
int i = x->n - 1;
// 情况 1:叶子节点,直接插入
if (x->leaf) {
while (i >= 0 && k < x->keys[i]) {
x->keys[i + 1] = x->keys[i];
i--;
}
x->keys[i + 1] = k;
x->n++;
}
// 情况 2:内部节点,递归下降
else {
while (i >= 0 && k < x->keys[i])
i--;
i++;
// 若目标子节点已满,先分裂
if (x->child[i]->n == 2 * T - 1) {
btree_split_child(x, i);
// 分裂后决定走左还是右
if (k > x->keys[i])
i++;
}
btree_insert_nonfull(x->child[i], k);
}
}
/*
* 插入入口
*
* 若根节点满:
* 1. 创建新根
* 2. 分裂旧根
* 3. 从新根插入
*/
void btree_insert(BTreeNode** root, int k) {
BTreeNode* r = *root;
if (r->n == 2 * T - 1) {
BTreeNode* s = btree_create_node(false);
s->child[0] = r;
*root = s;
btree_split_child(s, 0);
btree_insert_nonfull(s, k);
} else {
btree_insert_nonfull(r, k);
}
}
/* ================= 删除相关辅助函数 ================= */
/*
* 获取前驱(左子树最大值)
*/
int btree_get_pred(BTreeNode* x, int idx) {
BTreeNode* cur = x->child[idx];
while (!cur->leaf)
cur = cur->child[cur->n];
return cur->keys[cur->n - 1];
}
/*
* 获取后继(右子树最小值)
*/
int btree_get_succ(BTreeNode* x, int idx) {
BTreeNode* cur = x->child[idx + 1];
while (!cur->leaf)
cur = cur->child[0];
return cur->keys[0];
}
/*
* 合并 child[idx] 和 child[idx+1]
* 并将 x->keys[idx] 下沉
*/
void btree_merge(BTreeNode* x, int idx) {
BTreeNode* c = x->child[idx];
BTreeNode* s = x->child[idx + 1];
// 中间 key 下沉
c->keys[T - 1] = x->keys[idx];
// 拷贝兄弟节点的 key
for (int i = 0; i < s->n; i++)
c->keys[i + T] = s->keys[i];
// 拷贝子指针
if (!c->leaf) {
for (int i = 0; i <= s->n; i++)
c->child[i + T] = s->child[i];
}
// 父节点 key / child 左移
for (int i = idx + 1; i < x->n; i++)
x->keys[i - 1] = x->keys[i];
for (int i = idx + 2; i <= x->n; i++)
x->child[i - 1] = x->child[i];
c->n += s->n + 1;
x->n--;
free(s);
}
/*
* 删除核心递归函数
*/
void btree_remove(BTreeNode* x, int k);
/*
* 从节点中删除已命中的 key
*/
void btree_remove_from_node(BTreeNode* x, int idx, int k) {
// 情况 1:叶子节点,直接删除
if (x->leaf) {
for (int i = idx + 1; i < x->n; i++)
x->keys[i - 1] = x->keys[i];
x->n--;
}
// 情况 2:内部节点
else {
// 用前驱替换
if (x->child[idx]->n >= T) {
int pred = btree_get_pred(x, idx);
x->keys[idx] = pred;
btree_remove(x->child[idx], pred);
}
// 用后继替换
else if (x->child[idx + 1]->n >= T) {
int succ = btree_get_succ(x, idx);
x->keys[idx] = succ;
btree_remove(x->child[idx + 1], succ);
}
// 两边都不足,合并
else {
btree_merge(x, idx);
btree_remove(x->child[idx], k);
}
}
}
/*
* 删除递归主体
*
* 关键原则:
* 在向下递归前,保证目标子节点至少有 T 个 key
*/
void btree_remove(BTreeNode* x, int k) {
int idx = 0;
// 找到第一个 >= k 的 key
while (idx < x->n && x->keys[idx] < k)
idx++;
// 情况 1:key 在当前节点
if (idx < x->n && x->keys[idx] == k) {
btree_remove_from_node(x, idx, k);
}
// 情况 2:key 不在当前节点
else {
if (x->leaf)
return;
// 保证下降的子节点不少于 T 个 key
if (x->child[idx]->n < T) {
// 向左兄弟借
if (idx > 0 && x->child[idx - 1]->n >= T) {
BTreeNode* c = x->child[idx];
BTreeNode* s = x->child[idx - 1];
for (int i = c->n; i > 0; i--)
c->keys[i] = c->keys[i - 1];
c->keys[0] = x->keys[idx - 1];
x->keys[idx - 1] = s->keys[s->n - 1];
if (!c->leaf) {
for (int i = c->n + 1; i > 0; i--)
c->child[i] = c->child[i - 1];
c->child[0] = s->child[s->n];
}
c->n++;
s->n--;
}
// 向右兄弟借
else if (idx < x->n && x->child[idx + 1]->n >= T) {
BTreeNode* c = x->child[idx];
BTreeNode* s = x->child[idx + 1];
c->keys[c->n] = x->keys[idx];
x->keys[idx] = s->keys[0];
for (int i = 1; i < s->n; i++)
s->keys[i - 1] = s->keys[i];
if (!s->leaf) {
c->child[c->n + 1] = s->child[0];
for (int i = 1; i <= s->n; i++)
s->child[i - 1] = s->child[i];
}
c->n++;
s->n--;
}
// 借不了就合并
else {
if (idx < x->n)
btree_merge(x, idx);
else
btree_merge(x, idx - 1);
}
}
btree_remove(x->child[idx], k);
}
}
/*
* 删除入口(处理根节点退化)
*/
void btree_delete(BTreeNode** root, int k) {
if (!*root)
return;
btree_remove(*root, k);
// 根节点没有 key 且不是叶子,则树高降低
if ((*root)->n == 0 && !(*root)->leaf) {
BTreeNode* old = *root;
*root = (*root)->child[0];
free(old);
}
}
/*
* 测试程序
*/
int main() {
BTreeNode* root = btree_create();
int data[] = {10, 20, 5, 6, 12, 30, 7, 17};
for (int i = 0; i < 8; i++)
btree_insert(&root, data[i]);
btree_delete(&root, 6);
btree_delete(&root, 7);
btree_delete(&root, 12);
if (btree_search(root, 10))
printf("found 10\n");
return 0;
}