红黑树

可视化：https://www.cs.usfca.edu/~galles/visualization/RedBlack.html

平衡二叉树（AVL树）可以保证在最坏的情况下，查找、插入和删除的时间复杂度均为O(logn)。但是插入和删除后重新调整平衡可能需要多大O(logn)次旋转，频繁地调整平衡导致全树整体拓扑结构地变化。AVL树地左右子树高度差绝对值不超过1，而红黑树在AVL树“适度平衡”的基础上，进一步放宽条件：

红黑树的左右子树高度差不超过两倍。

红黑树也是一种平衡二叉搜索树，虽然和AVL树一样，查找、插入和删除的时间复杂度均为O(logn)，但其统计性能更好一些，不需要频繁调整平衡，任何不平衡都可以在3次旋转之内解决。

因此红黑树被广泛应用，例如 C++ STL set、multiset、map、multimap 都应用了红黑树的变体。

容器	底层结构	是否有序	是否允许重复	查找复杂度
vector	连续数组	❌	✔	O(1)
list	双向链表	❌	✔	O(n)
deque	分段连续数组	❌	✔	O(1)
set	红黑树	✔	❌	O(log n)
multiset	红黑树	✔	✔	O(log n)
map	红黑树	✔	❌	O(log n)
multimap	红黑树	✔	✔	O(log n)
unordered_set	哈希表	❌	❌	平均 O(1)
unordered_multiset	哈希表	❌	✔	平均 O(1)
unordered_map	哈希表	❌	❌	平均 O(1)
unordered_multimap	哈希表	❌	✔	平均 O(1)
queue	deque（默认）	❌	✔	❌（不支持查找）
stack	deque（默认）	❌	✔	❌（不支持查找）

红黑树的定义

红黑树（red-black tree）是满足以下性质的二叉搜索树。

每个节点是红色或黑色的
根节点是黑色的
每个叶子节点是黑色的
如果一个节点为红色，其孩子节点必为黑色
从任一节点到其后代叶子的路径上，均包含相同数目的黑节点。

黑高：从某节点x（不包含该节点）到叶子的任意一条路径上黑色节点的个数称为该节点的黑高。

红黑树的黑高：红黑树的黑高为根节点的黑高

红黑树的插入、删除等操作中，必须维护红黑树的5个性质，性质1，3很容易满足，需要特别维护性质2，4，5，即根为黑色，红节点必有黑孩子，左右子树黑高相同。

树高与性能

红黑树没有AVL树那么“平衡”，为什么查找、插入和删除的速度也为O(logn)呢？

这是因为含有n个内部节点的红黑树的高度不超过O(logn)

查找、插入、删除等操作都沿着从根到叶子的路径进行，因此其时间复杂度取决于树的高度。

只需证明：

$h = O(\log n)$

其中：

(h)：红黑树的高度
(n)：节点总数

定义：

$bh(x) = \text{从节点 } x \text{ 到叶子路径上的黑色节点数}$

称为节点 (x) 的 黑高（black-height）。

树高与黑高的关系

由于不存在连续的红色节点，在最坏情况下，从根到叶子的路径颜色交替出现：

$\text{黑} \rightarrow \text{红} \rightarrow \text{黑} \rightarrow \text{红} \rightarrow \cdots$

因此，路径上红色节点的数量不会超过黑色节点数量。

得到：

$h \le 2 \cdot bh(\text{root})$

黑高与节点数量的关系

命题： 任意一棵黑高为 (bh) 的红黑树，至少包含：

$n \ge 2^{bh} - 1$

证明（数学归纳法）：

基础情况： 当 (bh = 0) 时，树为空

$n = 0 = 2^0 - 1$

归纳假设： 黑高为 (k) 的红黑树至少有

$2^k - 1 \text{ 个节点}$

归纳步骤： 黑高为 (k+1) 的树，其根为黑色，左右子树黑高均为 (k)：

$n \ge 1 + (2^k - 1) + (2^k - 1) = 2^{k+1} - 1$

命题得证。

推导树高的上界

由上式：

$n \ge 2^{bh} - 1$

可得：

$bh \le \log_2 (n + 1)$

结合之前得到的不等式：

$h \le 2 \cdot bh$

代入得：

$h \le 2 \log_2 (n + 1)$

结论

红黑树的高度满足：

$h = O(\log n)$

因此，红黑树的基本操作时间复杂度为：

$\boxed{ \begin{aligned} \text{查找} &= O(\log n) \ \text{插入} &= O(\log n) \ \text{删除} &= O(\log n) \end{aligned} }$

红黑树与4阶B树

红黑树和4阶B树之间存在等价关系，如果从红黑树的树根开始，自顶向下逐层检查，如果遇到红节点，则将该节点压缩到父节点一侧；如果遇到黑节点，则保留。因为红节点对黑高没有贡献，而黑节点对黑高有贡献。

红黑树与4阶B树的4种等价方式。

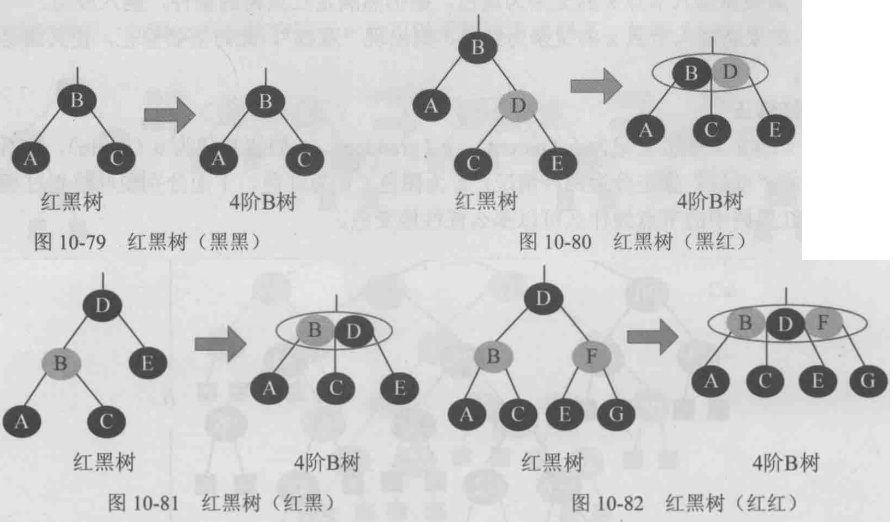
从红黑树与4阶B树的等价关系可以看出，4阶B树中的节点中必然含有一个黑节点，且最多包含3个关键字；如果包含2个红关键字，则黑关键字必然在中间位置。

为什么就这4种情况，因为这是红黑树的定义决定的。根节点为黑色，如果孩子有一个是黑节点，那么另一个分支黑高应该相同，如图一中的黑黑就满足，如果有一个孩子黑节点，另一个孩子为红节点，那么红节点必须补充两个黑色孩子节点才行，形成了图二和图三的情况，还有一种是两个孩子都是红孩子，有定义叶子节点必须为黑节点，所以红色孩子节点必须有两个黑节点，所以就形成了图四的情况。

不要思考太多，毕竟定义就是这样的。满足定义才能使得树比较平衡。

查找

红黑树本身就是“适度平衡”的二叉搜索树，其查找和二叉搜索树的查找一样。

插入

首先二叉搜索树，插入新节点，肯定是把节点插入到树中作为一个新的叶子节点，然后考虑树的平衡问题。

在红黑树中插入x，首先通过查找，如果查找成功，什么也不做，直接返回。如果查找失败，则在查找失败的位置创建x节点，并置为红色（如果为树根，则置黑色）

为什么插入的新节点一定要置红色？

如果置黑色则有可能改变黑高，违反性质5，如果置红色，不会改变黑高，但可能违反性质4（红色点必然有黑孩子）

插入分两种情况：

如果新插入节点x的父亲为黑色，则仍然满足红黑树的条件，插入成功
如果新插入节点x的父亲为红色，则出现双红，此时需要修正，使其满足红黑树的条件。

u为黑色

LL:x及其父亲p出现双红

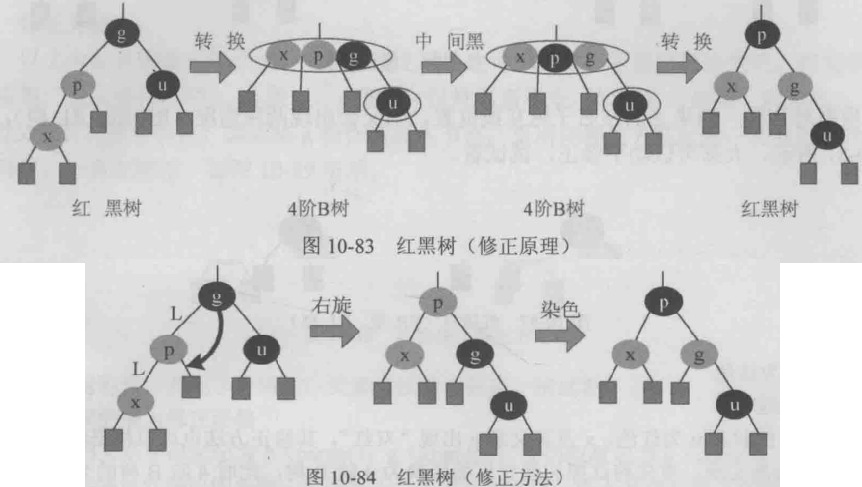
LR:x为p的右孩子

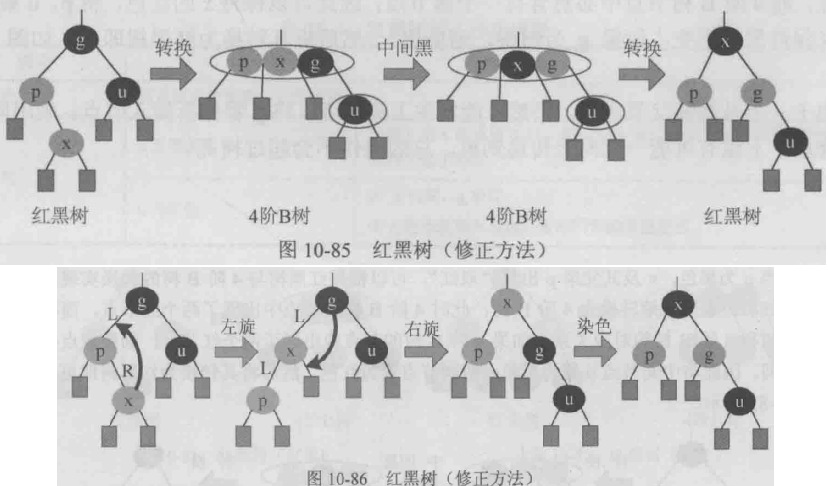
根据对称性，如果g的左右子树互换位置，则又会出现两种情况(RR型、RL型)。

u为红色

如果x的叔叔u为红色，x及其父亲p出现双红，转为4阶B树，出现上溢，执行分裂操作。

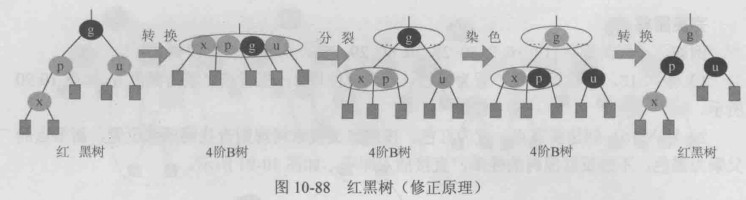
根据对称性，其他3种情况，都类似。

红黑树插入修正秘籍

情况	修正方法
p为黑色	满足红黑树性质，无需修正
p为红色，u为黑色	判断g到x的路径为LL、RR、LR、RL执行旋转，旋转后的根染黑，其两个孩子染红
p为红色，u为红色	p、u染黑，g染红，将g看作新插入节点，采取同样的方法处理

插入样例

一列关键字 {12,16,2,30,28,20,60,29,85}

删除

在红黑树种删除x，首先通过查找，如果查找失败，什么也不做，直接返回。
如果查找成功，则需要判断后处理，
- 如果x节点仅有左子树或右子树，则删除x，令其左子树或右子树子承父业代替位置。
- 如果x节点有左子树和右子树，则令x的直接前驱（或直接后继）代替其位置，然后删除其直接前驱或直接后继即可，在删除节点的过程中，有可能违反红黑树的性质2、4、5，即根为黑色，红节点必有黑孩子，左右子树黑高相等，简而言之，跟为黑、无双红、黑高相等。

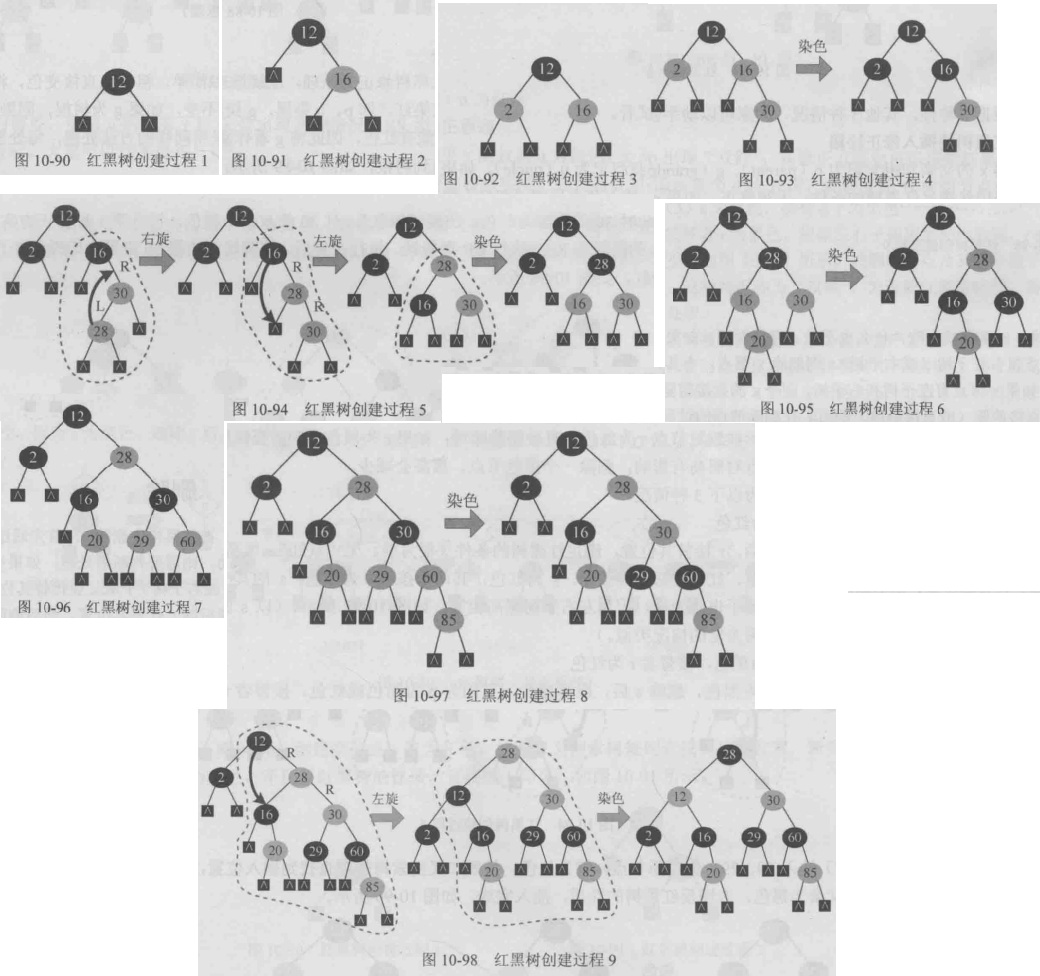
注意：如果x节点有左子树和右子树，则实际被删除节点为其直接前驱（或直接后继）。要删除的节点的关键字直接替换为直接前驱（或直接后继）中的关键字，其他啥都不用做，然后把直接前驱（或直接后继）那个节点删掉。

要删除节点x，令r指向实际被删除节点s的接替者，p指向x的父亲，s必有一个孩子为空。

如果实际被删除节点s为红色，直接删除即可；如果s为黑色，则需要根据情况修正，因为黑色节点对黑高有影响，删除一个黑色节点，黑高会减少。

有三种情况

s为红色

删除s后，r接替其位置，满足红黑树的条件（根为黑、无“双红”、黑高不变）。根据红黑树的性质，红节点必有黑孩子，s为红色，其两个孩子必为黑色，s的其中一个孩子为空，另一个孩子也必为空，因为左右子树黑高相等。（下面的是以s的右子树为空为例，左子树为空的情况类似）

s为黑色，接替者r为红色

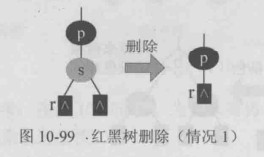
因为s为黑色，删除s后，黑高减少。又因为p为黑色或红色，接替者r为红色，有可能出现“双红”。可以直接将r置为黑色，既维护了黑高（删除一个黑色的s，置r为黑色，黑高不变），又避免了“双红”。

下图是s右子树为空情况，左子树为空情况类似。

s为黑色，接替者r为黑色

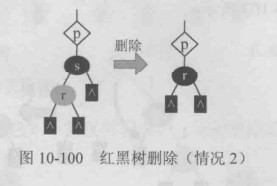
接替者r为黑色，根据左右子树黑高相同原则，r必为空，因为s为黑色，删除s后，黑高减少。下图，被删除节点及其两个孩子都为黑色，这种情况称为“双黑”，为维护红黑树特性，需要分情况处理。

因为被删节点s为黑色，会产生黑高，因此s必然有兄弟，否则会违反左右子树黑高相同的特性。将s的兄弟记为 b(brother),s的父亲仍然为p，分为以下4种情况处理。

b为黑色，b有红孩子(BB-1)

首先将红黑树通过压缩转换为4阶B树，删除s后，发生下溢（关键字个数不足），此时可以向做兄弟借一个关键字，即父亲下沉，左兄弟的最右关键字上移。而4阶B树的节点中必包含一个黑节点，因此节点t染为黑色，然后将其转换为红黑树即可，转换后满足红黑树条件（根为黑、无双红、黑高相等）。（长方块表示子树，黑高为0）。

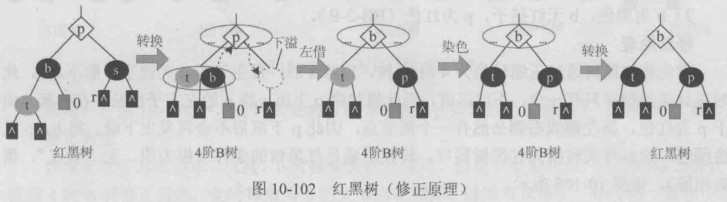
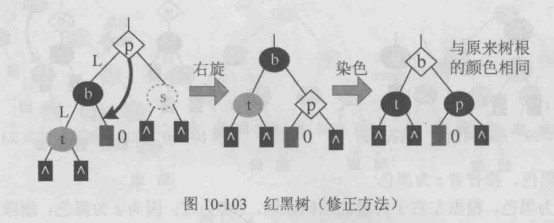
修正方法:可以看作旋转和染色的过程，p到b的红孩子之间路径为LL，执行右旋，将p右旋，旋转后的根保留原树根的颜色，其两个孩子染黑。

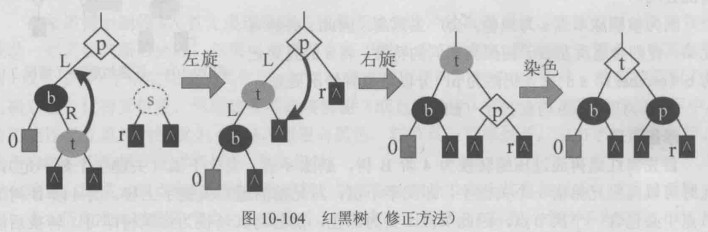
同样的道理，如果p到b的红孩子之间路径为LR、则先执行左旋，再执行右旋，最后染色即可

根据对称性，如果p的左右子树互换位置，则又会出现两种情况(RR型，RL型)，只是旋转不同而已，染色都是一样的。

b为黑色，b无红孩子，p为红色(BB-2-R)

首先将红黑树通过压缩转换为4阶B树，删除s后，发生下溢（关键字个数不足），此时左兄弟关键字只有一个，不可以借，因此将父亲p下沉，将p的左右子树粘合在一起。由于p为红色，其左侧或右侧必然有一个黑节点，因此p下沉后不再会发生下溢。将b、p互换颜色，然后将其转换为红黑树即可。

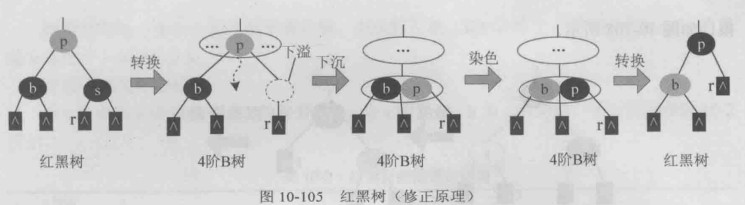
为什么将b、p互换颜色，不换色可以吗（旋转不如染色速度快）.

b为黑色,b红孩子,p为黑色(BB-2B)

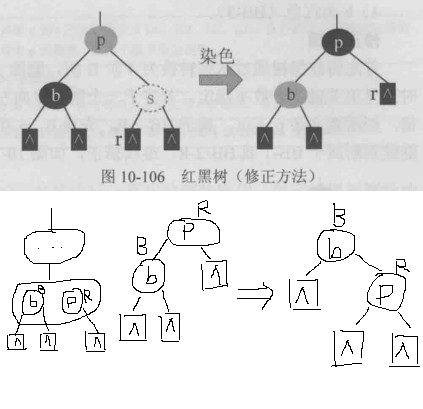
首先将红黑树通过压缩转换为4阶B树,删除s后,发生下溢(关键字个数不足),此时左兄弟关键字只有一个,不可以借, 因此将父亲p下沉,将p的左右子树粘合在一起.此时再次发生下溢,粘合后不满足4阶B树的要求(每个节点中有且只有一个黑色), 可以将b染红色,然后将其转换为红黑树. 此事等效为p的父亲被删除,继续做双黑修正,有可能一直向上传递,修正到树根.

为什么要将b染为红色?p染为红色可以吗?还是那样,染色比旋转快.

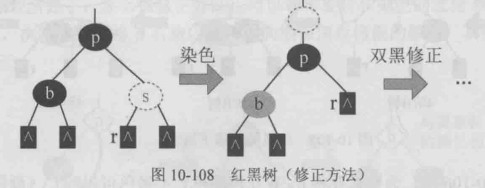
修正方法:该情况修正方法简单直接,b直接染为红色即可,但一定要注意,不能就这么停止, 根据4阶B树修正原理,此时等效为p的父节点被删除了,继续双黑修正,有可能一直到根.

b为红色(BB-3)

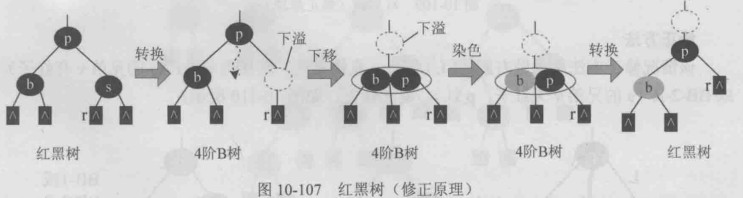
首先将红黑树通过压缩转换为4阶B树,删除s后,发生下溢(关键字不足),此时左兄弟关键字个数不确定,若多于一个则可以向左借,属于BB-1;若只有一个,不可以借,则需要父亲p下沉,属于BB-2-R.
先将b p互换颜色,然后将其转换为红黑树即可.

继续判断属于BB-1或BB-2-R,继续修正.

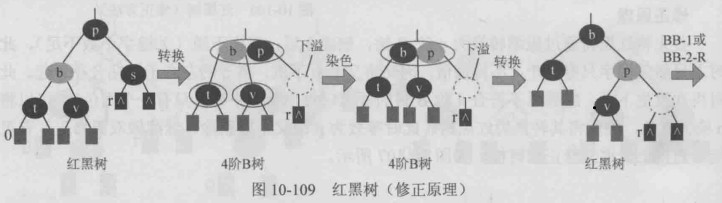
修正方法:

该情况修正首先做右旋(LL),b p直接换色,转换为BB-1(s的兄弟v有红子)或BB-2-R(s的兄弟v无红子,p红) 继续修正.

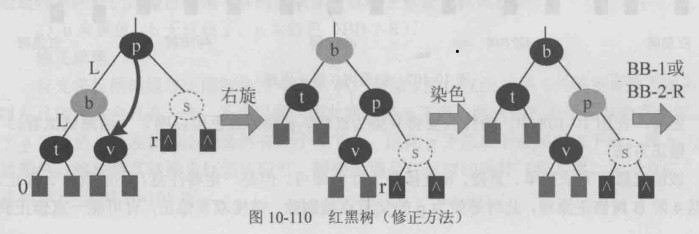
根据对称性,如果p的左右子树互换,则执行左旋(RR),染色,转换为BB-1(s的兄弟v有红子)或BB-2-R

红黑树删除修正秘籍

令r指向实际被删除节点s的接替者,p为s的父亲,b为s的兄弟

情况		修正方法
s红		满足红黑树性质,无需修正
s黑有红子r		r染为黑色
s黑无红子	b黑有红子t(BB-1)	判断p到t之间的路径为LL RR LR RL,执行旋转,旋转后根保留原来p的颜色,其两个孩子染为黑色
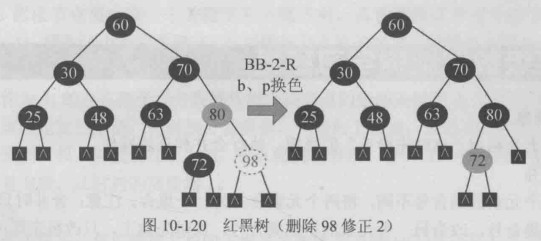
s黑无红子	b黑无红子p红(BB-2-R)	b p换色
s黑无红子	b黑无红子p黑(BB-2-B)	b染为红色,此时等效为p的父节点被删除,继续双黑修正
s黑无红子	b红(BB-3)	右旋或左旋,b p换色,转换为BB-1或BB-2-R,继续修正

删除图解

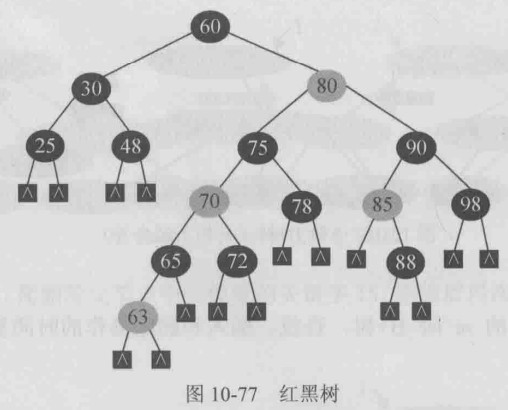
一棵红黑树如下,对其进行一系列的删除操作,展示红黑树删除的所有情况.

删除85, 85只有右子树,左树为空,且为红色,直接删除令右子树接替即可,满足红黑树条件(根为黑,无双红,黑高不变)

删除65,65只有左子树,右子树为空,且为黑色,有红子,直接删除令左子树接替, 红子63染黑,满足红黑树的条件

删除75,75的左右子树均有,因此找到75的前驱72(左子树最右节点),令72代替75,删除72即可, 实际被删除节点72为黑色且无红子,出现”双黑” 其兄弟也黑色无红字,父亲为红,符合 BB-2-R 型修正, 删除后,兄弟63和父亲70换色即可.

删除78,78为黑色且无红子,出现”双黑”,其兄弟也黑色有红子63,符合BB-1型修正,判断p到t之间的路径为LL,执行右旋,旋转后根保留原p的颜色,其两个孩子染为红色.

删除88,88为黑色且无红子,出现”双黑”,其兄弟也黑色无红子,父亲为黑,符合 BB-2-B 型修正,删除88后,兄弟98染红,此时等价为90的父亲(空节点)被删除,再次修正. 该空节点黑色无红孩子,出现”双黑”,其兄弟也黑色无红子,父亲为空,符合 BB-2-R 型修正,删除后兄弟70 和父亲 80换色.

删除90,90为黑子且有红子,删除后红子染黑即可,满足红黑树的条件

删除98,90为黑色且无红子,出现”双黑”,其兄弟为红色,符合BB-3型修正,先右旋,然后兄弟b 父亲p换色,此时转换为 BB-2-R(b无红子,p红),

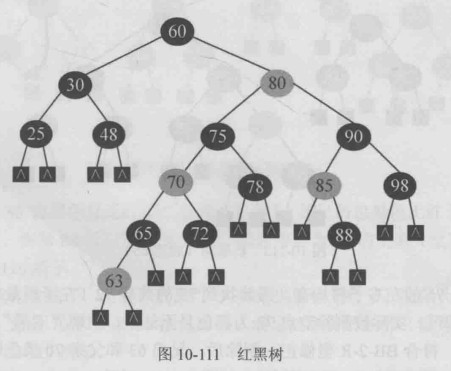
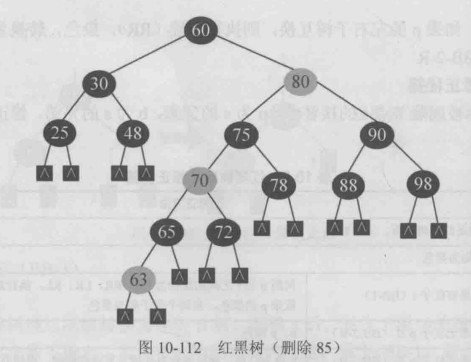
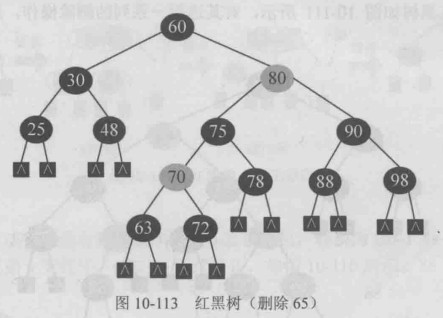
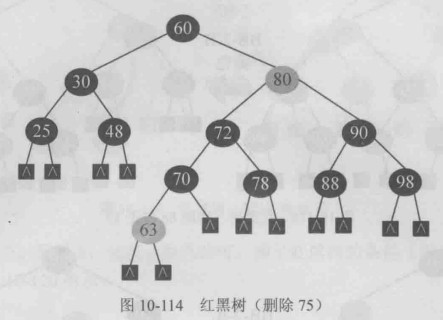
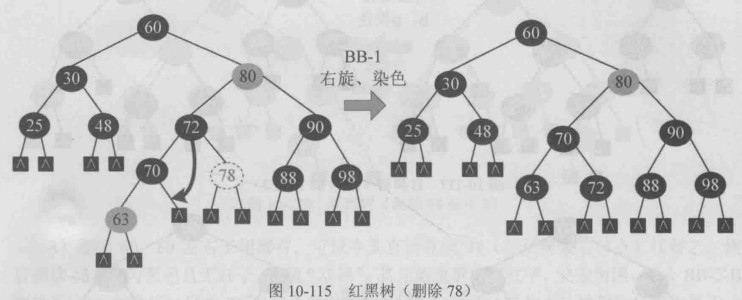
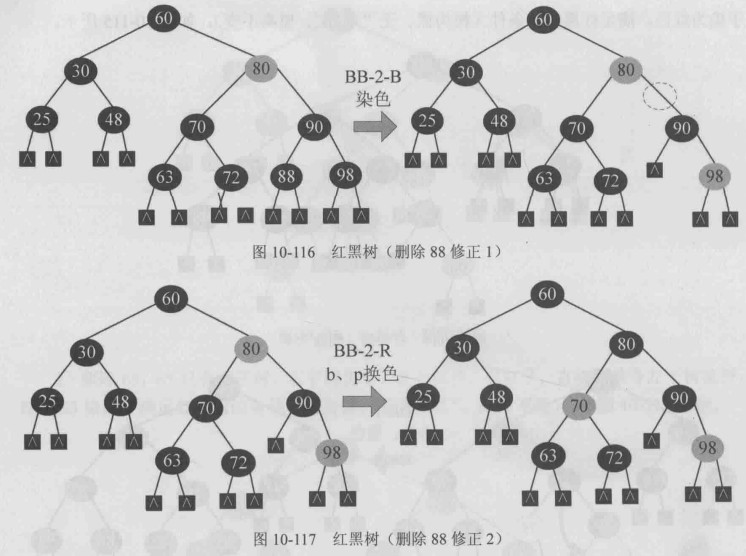
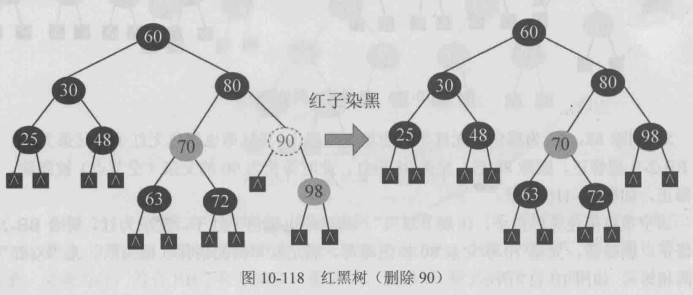
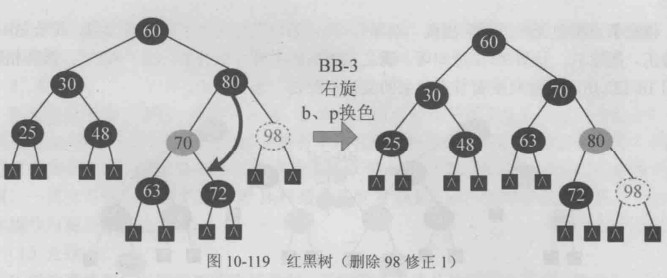
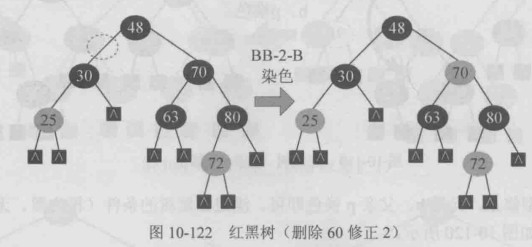
BB-2-R型修正,兄弟b 父亲p换色即可,满足红黑树的条件

删除60,60左右子树都有,可以令其直接前驱48(左子树最右节点)代替之,然后删除48, 48为黑色且无红子,出现”双黑”, 其兄弟也黑色无红子,父亲为黑,符合 BB-2-B 型修正,48删除后,兄弟25 染红,此时等价为30的父亲(空节点)被删除,再次修正

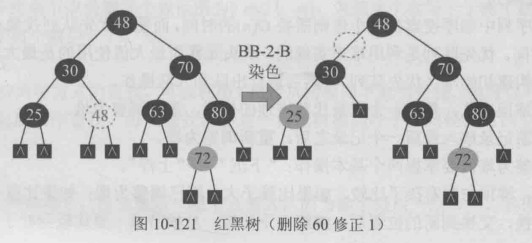
该空节点黑色无红孩子,出现”双黑”,其兄弟也黑色无红子,父亲为黑,符合 BB-2-B型修正,删除后,兄弟70染色即可,满足红黑树的条件,此时被删除节点的父亲的父亲不存在,迭代停止.