优先队列

算法设计中，经常用到从序列找一个最小值（或最大值）的操作，如果从序列中顺序查找最小值（或最大值）需要 O(n) 的时间，而使用优先队列找最小值（或最大值）则只需要 O(logn)的时间。

优先队列是利用堆来实现的，堆可以看作一棵完全二叉树的顺序存储结构，在这棵完全二叉树中，如果每一个节点的值都大于等于左右孩子的值，则称为最大堆，如果每一个节点的值都小于等于等于左右孩子的值，则称为最小堆。

根据完全二叉树的性质，如果一个节点的下标为i，则其左孩子下标为 2i,其右孩子下标为 2i+1， 其双亲的下标为i/2。且有n个节点的完全二叉树深度为 floor(log2n)+1

普通的队列是先进先出的，而优先队列与普通队列不同，每次出队列时按照优先级顺序出队。 例如，最小值（或最大值）出队，优先队列中的记录存储满足堆的定义，优先队列除了构建初始堆之外， 有出队和入队两种常用的操作。

算法步骤：

1. 构建初始堆
2. 出队：堆顶出队，最后一个记录代替堆顶的位置，重新调整为堆
3. 入队：新纪录放入最后一个记录之后，重新调整堆

出队

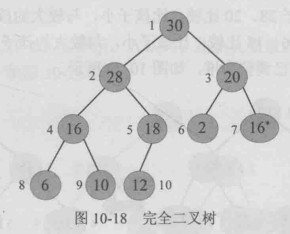
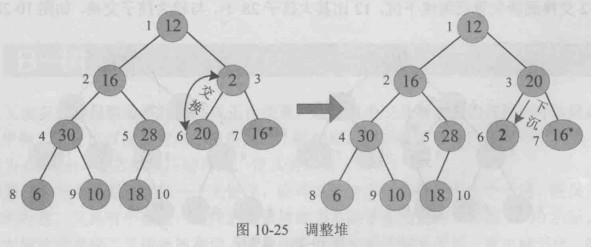
例如，一个最大堆，出队时，堆顶30出队，最后一个记录12代替堆顶。

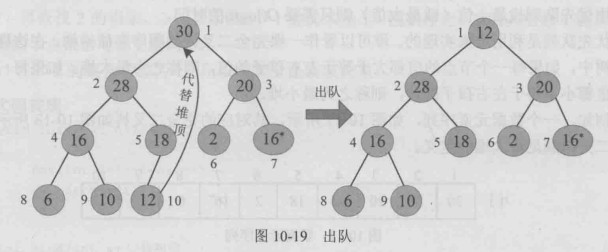
出队后，除了堆顶之外，其他节点都满足最大堆的定义，只需要将堆顶执行“下沉”操作，即可调整为堆。

“下沉”：堆顶与左右孩子比较，如果比孩子大，则已调整为堆，如果比孩子小，则与较大的孩子交换，交换到新的位置后， 继续向下比较，从根节点一直比较叶子。

1. 堆顶12和两个孩子28、20比较，比孩子小，与较大的孩子28交换。
2. 12再和两个孩子16、18比较，比孩子小，与较大的孩子18交换。
3. 比较到叶子停止，已调整为堆

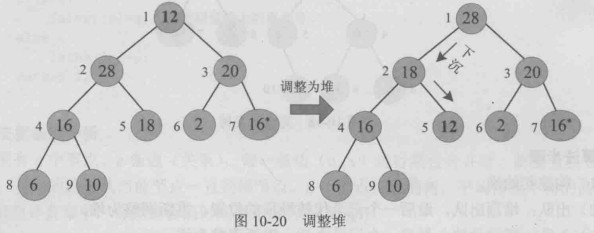
调整堆的过程就是堆顶从根“下沉”到叶子的过程。

void Sink(int k, int n) // 下沉操作
{
    while (2 * k <= n) // 如果有左孩子,k的左孩子为2k,右孩子为2k+1
    {
        int j = 2 * k;                // j 指向左孩子
        if (j < n && r[j] < r[j + 1]) // 如果有右孩子,且左孩子比右孩子小
            j++;                      // j 指向右孩子
        if (r[k] >= r[j])             // 比“较大的孩子”大
            break;                    // 已满足堆
        else
            swap(r[k], r[j]); // 与较大的孩子交换
        k = j;                // k指向交换后的新位置,继续向下比较,一直“下沉”到叶子
    }
}

void pop(int n) // 出队
{
    cout << r[1] << endl; // 输出堆顶
    r[1] = r[n--];        // 最后一个元素代替堆顶,n减1
    Sink(1, n);           // 堆顶下沉操作
}

入队

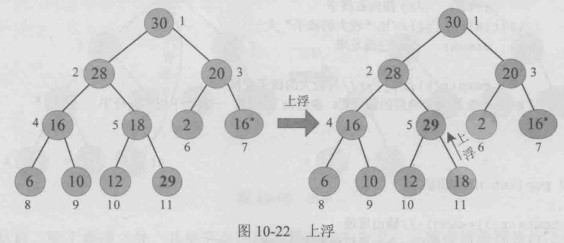
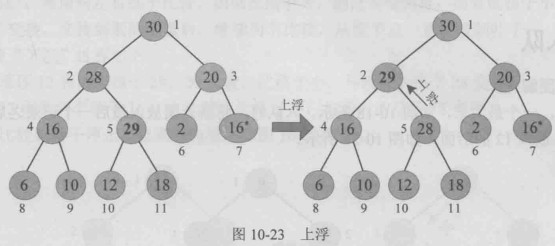
如果，一个最大堆，入队时，将新元素放入最后一个记录之后，例如29入队，放入12的后面。

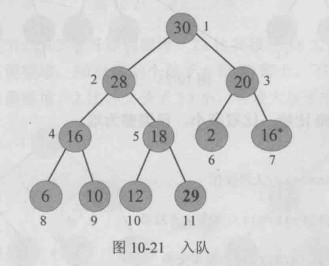
入队后除了新入队记录之外，其他节点都满足最大堆的定义，只需要将新记录执行“上浮”操作，即可调整为堆。

“上浮”：新记录与其双亲比较，如果小于等于双亲，则已调整为堆，如果比双亲大，则与双亲交换，交换到新的位置后，继续向上比较，从叶子一直比较到根。

void Swim(int k, int n) // 上浮操作
{
    while (k > 1 && r[k] > r[k / 2]) // 如果大于双亲
    {
        swap(r[k], r[k / 2]); // 与双亲交换
        k = k / 2;            // k 指向交换后的新位置，继续向上比较，直到上浮到根
    }
}

void push(int n, int x) // 入队
{
    r[++n] = x; // n 加 1 后，将新元素放入尾部
    Swim(n);    // 最后一个元素上浮操作
}

构建初始堆

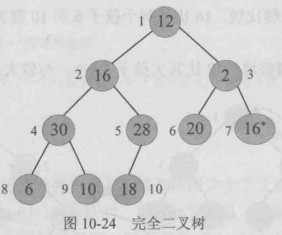
例如，对五序序列 {12, 16, 2, 30, 28, 20, 16*, 6, 10, 18} 构建初始堆（最大堆）。

构建初始堆过程：首先按照完全二叉树的顺序构建一棵完全二叉树，然后从最后一个分支节点 n/2 开始调整堆， 依次将序号为 n/2-1, n/2-2, ... 1 的节点执行下沉操作，调整为堆。

1. 将无序序列按照完全二叉树的顺序构建完全二叉树，
2. 从最后一个分支节点5开始调整堆，28比其孩子18都大，不需要交换。
3. 下标为4的节点调整堆，30比其两个孩子6和10都大，不需要交换。
4. 下标为3的节点调整堆，2比其大孩子20小，与较大孩子交换

5. 序号为2的节点调整堆，16比其大孩子30小，与较大孩子交换，继续下沉，交换到新位置后继续比较，16比其两个孩子6和10都大，不需要交换，比较到叶子停止。
6. 序号1的节点进行下沉操作，调整堆。

void CreateHeap(int n) // 构建初始堆
{
    // 从最后一个分支节点n/2开始下沉调整为堆，直到第一个节点
    for (int i = n / 2; i > 1; i--)
    {
        Sink(i, n);
    }
}

算法复杂度分析

优先队列是利用堆实现的一种特殊队列，堆是按照完全二叉树顺序存储的，具有n个节点的完全二叉树的深度为 floor(log2n) + 1。出队时，堆顶元素出队，最后一个元素代替堆顶，新的堆顶从跟下沉到叶子，最多达到树的深度，时间复杂度为O(logn)，入队时，新元素从叶子上浮到根，最多达到树的深度，时间复杂度也为 O(logn)。优先队列的入队和出队操作复杂度均为O(logn)。因此在n个元素的优先队列中找到一个最小值（或最大值）的时间复杂度为(O(logn))。想找到一个最大值就用最大堆，想找到一个最小值就用最小堆。